Classic horns

---

Theoretical horns

Classic horns are those with a single exterior surface (i.e., a surface that can be described by a single mathematical equation) and whose theoretical performance can be mathematically derived from the one-dimensional wave equation (ignoring all effects from Poisson's ratio). Classic horns include prismatic (unshaped), exponential, catenoidal, and tapered.

(Note — There are other surface equations, such polynomials, that can describe a single surface. However, the one-dimensional wave equation may not be solvable for such surfaces.)

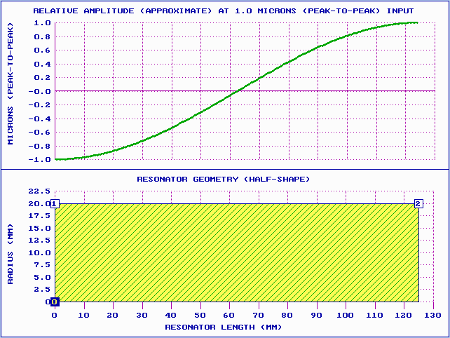
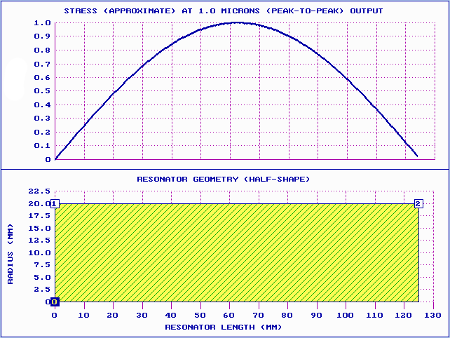
Prismatic (unshaped)

Amplitude Stress (relative)

Figure 1. Prismatic horn performance

Details ...

Tapered

Amplitude Stress (relative)

Figure 2. Tapered horn performance (theoretical)

Exponential

Amplitude Stress (relative)

Figure 3. Exponential horn performance (theoretical)

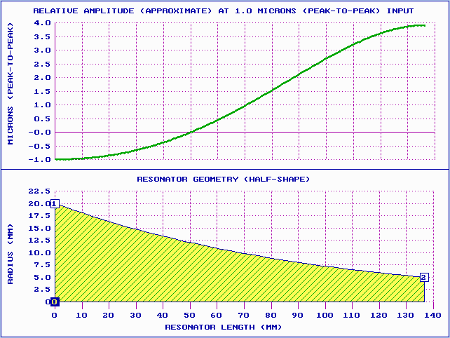
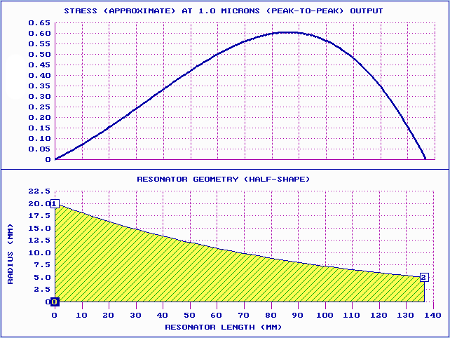
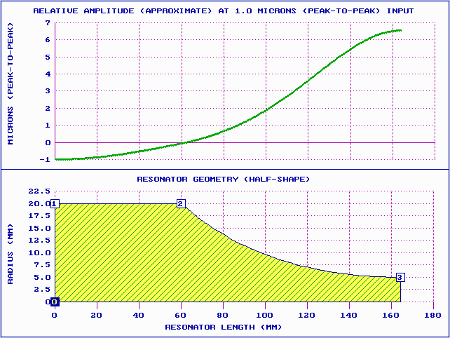
Catenoidal

Amplitude Stress (relative)

Figure 4. Catenoidal horn performance (theoretical)

Performance comparisons

Table 1. Performance comparisons

Horn Tuned length Gain Relative stress Prismatic 1.00 1.00 1.00 Tapered 1.16 3.15 0.57 Exponential 1.09 4.00 0.60 Catenoidal 1.02 5.15 0.66

Table notes —

1. All values for the prismatic horn have nominal values of 1.00 nondimensional units. Then the performance of the other horns can be directly compared to the nominal prismatic horn. For example, length of the tapered horn is 16% higher than the prismatic horn and the gain is 3.15 greater.
2. The amplitudes are relative to a common input amplitude of 1.0. Then the horn gain is just the right-most amplitude on the amplitude graph (i.e., the output amplitude).
3. The stresses are relative to a common output amplitude (rather than the input amplitude) since this is the amplitude that performs the application. For example, for the same output amplitude the the stress in the tapered horn is 57% as great (i.e., 43% lower) as the prismatic horn.
4. Although the performances in the table were determined for 20 kHz example horns, the comparative performances will be the same at any frequency.
5. The graphed results are labeled as "approximate" because of the way they were determined. However, these results are very close to the theoretical values.

Practical horns

The above theoretical horns are not practical because they don't have means to tighten them to another resonator (e.g., spanner wrench holes or wrench flats). The tightening means typically require a prismatic shoulder at the back of the horn. For traditional tapered and exponential horns these shoulders have typically been fairly short (e.g., 12 mm for a 20 kHz horn). Such short shoulders would not have a significant impact on the horn's performance.

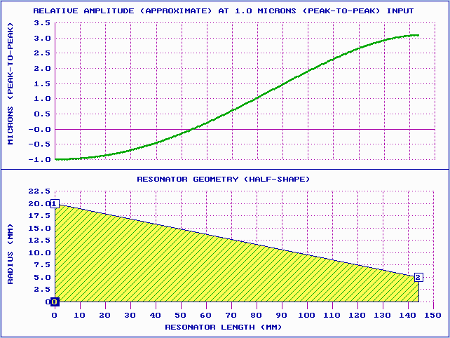
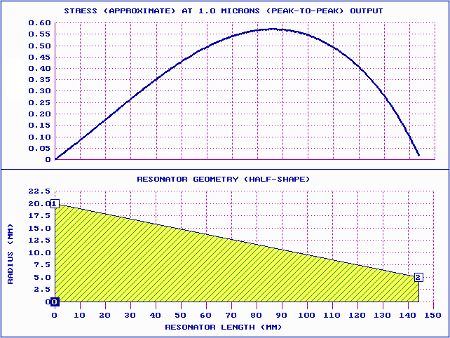
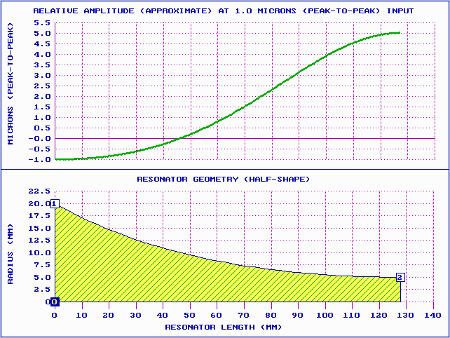
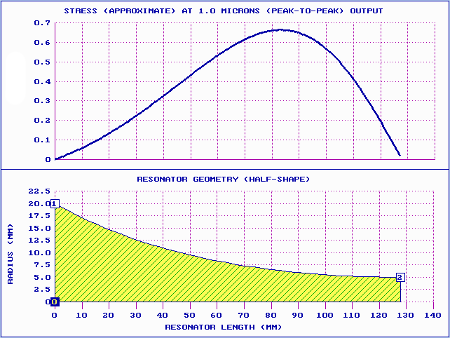
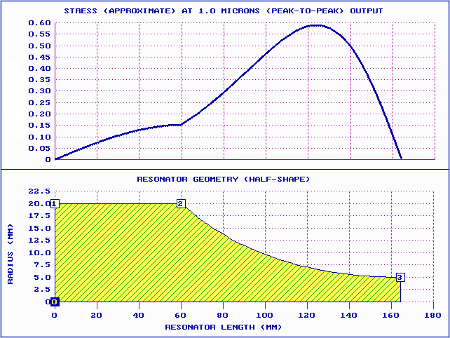
On the other hand, catenoidal horns have generally had very long shoulders, typically about a quarter wavelength (approximately 60 mm at 20 kHz for most acoustic materials). This will significantly affect the performance of the practical catenoidal horn compared to the theoretical catenoidal horn above.

Amplitude Stress (relative)

Figure 5. Catenoidal horn performance (20 kHz with 60 mm shoulder)

Table 2. Catenoidal horn performance comparisons (20 kHz without and with shoulders)

Horn Tuned length Gain Relative stress Catenoidal (no shoulder) 1.02 5.15 0.66 Catenoidal (60 mm shoulder) 1.31 6.54 0.60

---