Mechanical—Electrical analogs
Systems that oscillate mechanically or electrically have similar characteristics. This page will establish the mechanical-electrical analogs.
Mechanical oscillation
|
|
|
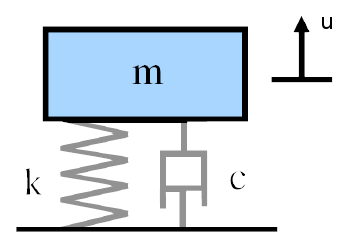
For the simple mass-spring-damper system of figure 1, the equation of motion is —
\begin{align} \label{eq:14801a} F(t) &= m \, \frac{d^2u}{dt^2} + c \, \frac{du}{dt} + k \, u \\[0.7em]%eqn_interline_spacing &= m \, \ddot{u} + c \, \dot{u} + k \, u \nonumber \end{align}
where —
| \( F(t) \) | = forcing function |
| \( u \) | = displacement |
| \( \frac{du}{dt} \) | = velocity (\(\dot{u}\)) |
| \( \frac{d^2u}{dt^2} \) | = acceleration (\(\ddot{u}\)) |
| \( m \) | = mass |
| \( c \) | = damping constant (viscous) |
| \( k \) | = spring stiffness |
Note: in mechanical systems various kinds of damping are possible. The above equation assumes viscous damping where the damping force is proportional to the velocity.
The energy stored in the moving mass due to its velocity is —
\begin{align} \label{eq:14802a} W_m = \frac{1}{2} \, m \, \dot{u}^2 \end{align}
The energy stored in the spring due to its stretch is —
\begin{align} \label{eq:14803a} W_k = \frac{1}{2} \, k \, u^2 \end{align}
The power dissipated by the damper is —
\begin{align} \label{eq:14804a} P_c = c \, \dot{u}^2 \end{align}
The resonant frequency is —
\begin{align} \label{eq:14805a} f = \sqrt\frac{k}{m} \end{align}
Electrical oscillation
|
|
|
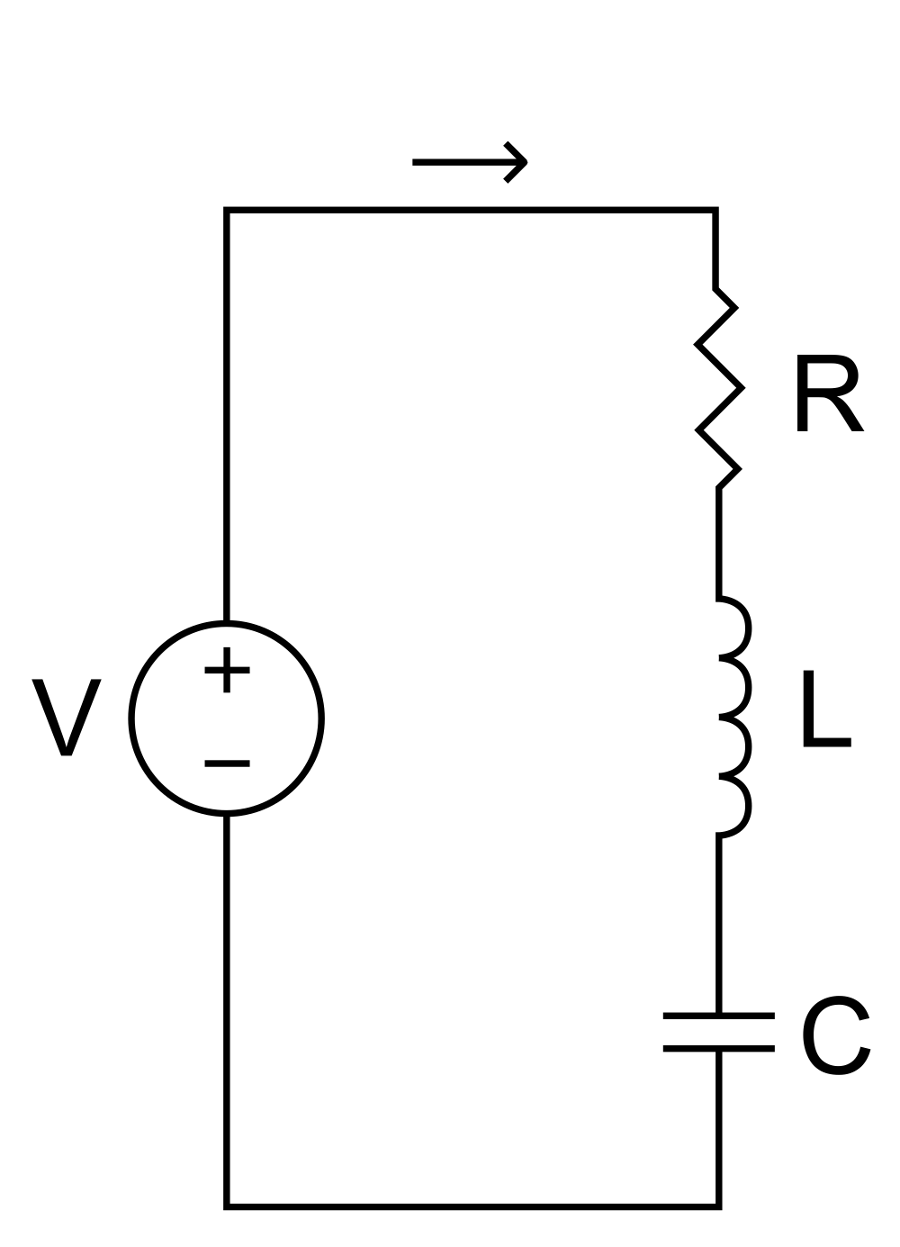
For the simple inductor-capacitor-resistor circuit of figure 2, the circuit equation is —
\begin{align} \label{eq:14820a} V(t) &= L \, \frac{d^2q}{dt^2} + R \, \frac{dq}{dt} + \frac{1}{C} \, q \\[0.7em]%eqn_interline_spacing &= L \, \ddot{q} + R \, \dot{q} + \frac{1}{C} \, q \nonumber \end{align}
where —
| \( V(t) \) | = voltage function |
| \( q \) | = charge |
| \( \frac{dq}{dt} \) | = current (\(\dot{q}\)) |
| \( \frac{d^2q}{dt^2} \) | = zzz (\(\ddot{q}\)) |
| \( L \) | = inductance |
| \( R \) | = resistance |
| \( C \) | = capacitance |
The energy stored in the inductor due to the moving charge is —
\begin{align} \label{eq:14851a} W_L = \frac{1}{2} \, L \, \dot{q}^2 \end{align}
The energy stored in the capacitor due to the stored charge is —
\begin{align} \label{eq:14852a} W_C = \frac{1}{2} \, \frac{1}{C} \, q^2 \end{align}
The power dissipated by the resistor is —
\begin{align} \label{eq:14853a} P_R = R \, \dot{q}^2 \end{align}
The resonant frequency is —
\begin{align} \label{eq:14854a} f = \sqrt\frac{1}{L \, C} \end{align}
Comparison
Comparing the corresponding mechanical and electrical equations, the following analogs are apparent. These analogs are particularly useful in discussing transducer equivalent circuits.
|
||||||||||||||
|
Note that the analog of the mechanical stiffness \( k \) is the reciprocal of the electrical capacitance \( 1/C \). Thus, increasing the capacitance reduces the stiffness. Hence the capacitance is also analagous to mechanical compliance.