Modal interaction

Overview

When two resonances are close together they may interact. This can distort the amplitude field of the primary resonance and/or may cause the power supply to jump to the secondary (parasitic) resonance.

Example

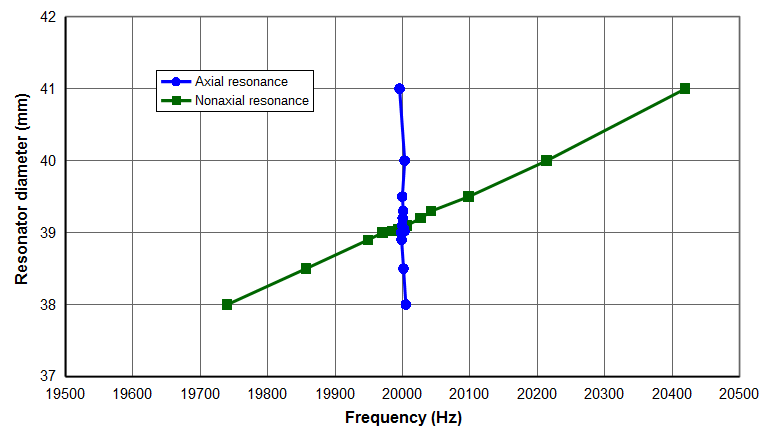
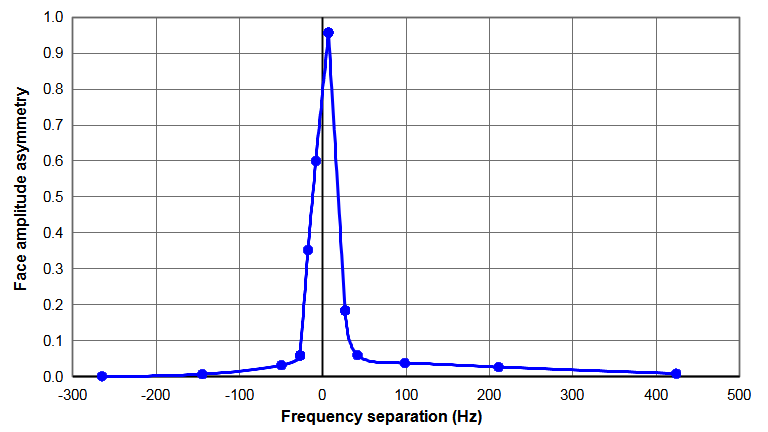
The following shows an example of modal interactions for a 20 kHz cylindrical prismatic horn (\( c_{tw} \) = 5100 m/sec; Poisson's ratio = 0.33). The horn's diamter was adjusted beetween 38 mm and 41 mm in order to affect the amount of modal interaction. The horn's length was adjusted slightly (between 126.54 mm and 126.62 mm) to maintain the axial resonance at 20 kHz. As expected, the modal interaction is greatest when the frequency separation is smallest. (Also see Amplitude asymmetry.)

Figure 1. Frequencies for a 20 kHz \( \phi \)40 mm horn

Figure 2. Face amplitude asymmetries for a 20 kHz \( \phi \)40 mm horn

 

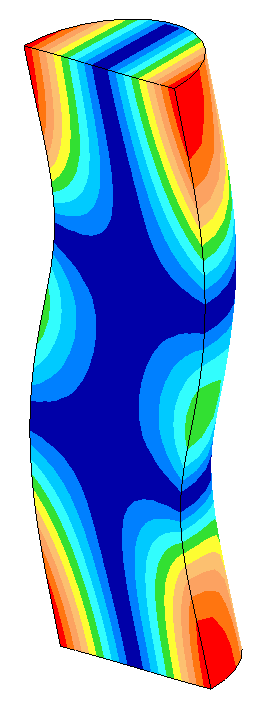
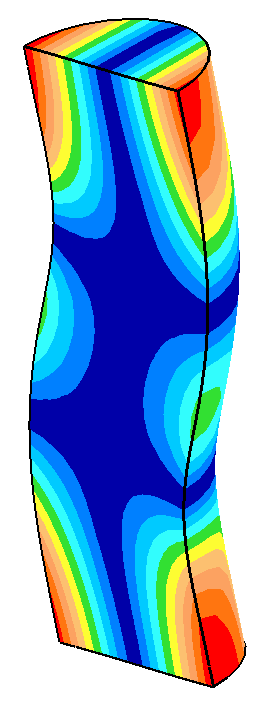
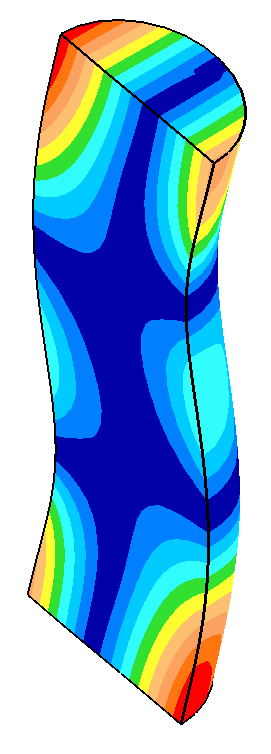
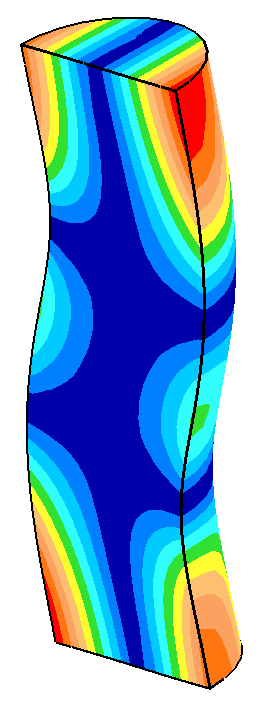
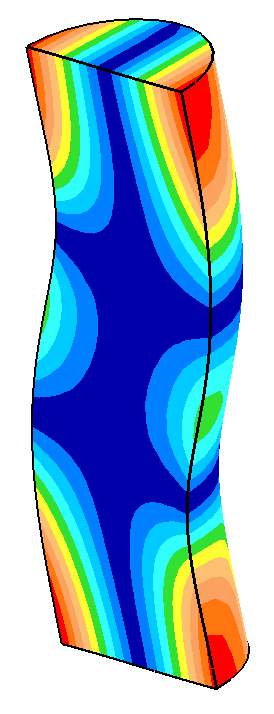
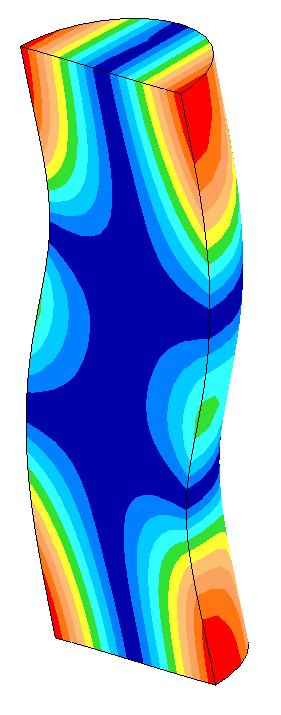
The following table shows some data from the above graphs. When the nonaxial (bending) mode is close to the axial resonance (low frequency separation), small changes in the horn's diameter cause large changes in the amplitude asymmetry. In particular, the face motion of the axial resonance starts to assume characteristics of the bending resonance. When the frequency separation is sufficiently large, the axial mode performs as if the bending mode were not present.

Table notes —

1. All displacements (as represented by the image colors) are in the axial direction.
2. All displacements are displayed at the same scale.

 

Diameter (mm)	Frequency separation (Hz)	Axial mode	Nonaxial mode
38.00	-265	20005 Hz Asymmetry = 0.001	19740 Hz
39.00	-27	20000 Hz Asymmetry = 0.06	19973 Hz
39.02	-18	19998 Hz Asymmetry = 0.34	19982 Hz
39.05	-12	20000 Hz Asymmetry = 0.50	19988 Hz
39.10	6	20000 Hz Asymmetry = 0.96	20006 Hz
39.20	27	20000 Hz Asymmetry = 0.18	20027 Hz
39.30	42	20001 Hz Asymmetry = 0.06	20043 Hz
41.00	424	19996 Hz Asymmetry = 0.008	20420 Hz

Suggested frequency separation

In an optimization of a 20 kHz 4.5" x 6" (114 mm x 152 mm) titanium block horn, O'Shea [1] (p. 260) specified a target frequency separation of at least 1200 Hz between the axial and nonaxial resonances. The reason for this target wasn't specified. If the reason was to avoid frequency jump then it should be noted that power supply controls have become much more sophisticated since this 1991 presentation so a narrower frequency range may be possible. In fact, horns having frequency separations of 500 Hz at 20 kHz have been successful.

Liesegang[1A], p.10 specified a frequency separation of 1000 Hz at 20 kHz. 

---