Piezoelectric transducer design (preliminary)
Contents
- Overview
- Langevin transducer
- Prestress designs
- Components
- Mechanical fits
- Assembly
- Transducer failure modes
- Testing prototype designs
- Performance
- Overcoming power limitations
- Appendices
- Appendix A: Comparison of 33 and 31 ceramic operation
- Appendix B: Manufacturer's piezoelectric cross-reference
- Appendix C: Method for applying prestress
- Appendix D: Ceramic dimensional specifications
- Appendix E: Ceramic electromechanical specifications
- Appendix F: Mechanical fits
- Appendix G: Understanding piezoelectric constants
- Appendix H: Effect of stack bolt on electromechanical coupling coefficient
- Appendix I: Resonance packet (pair)
- Appendix J: Comparison — series resonance and parallel resonance
- Figures
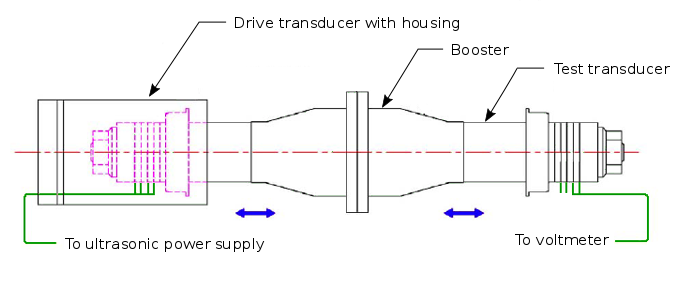
- Figure 1. 20 kHz industrial transducer with six piezoelectric ceramics (33 mode)
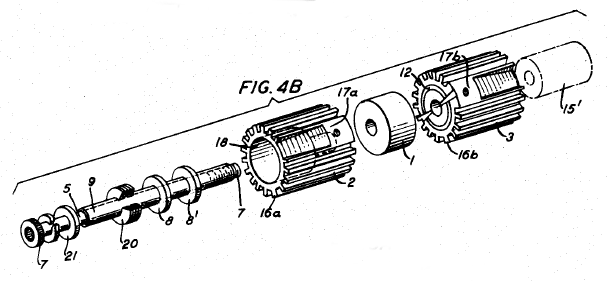
- Figure 2. Piezoelectric transducer components (center bolt design, 33 mode)
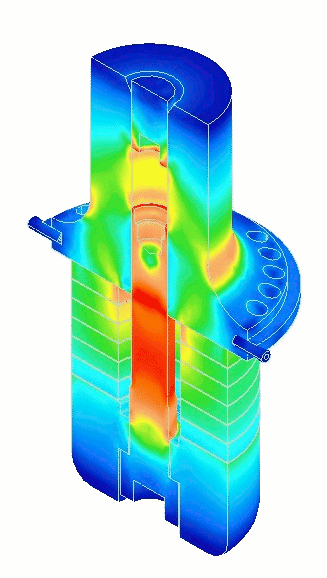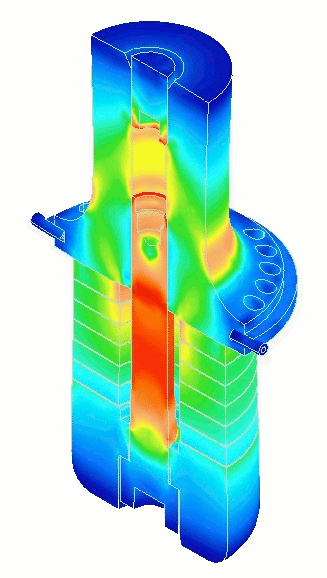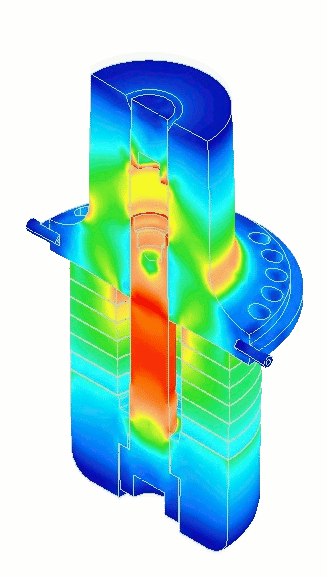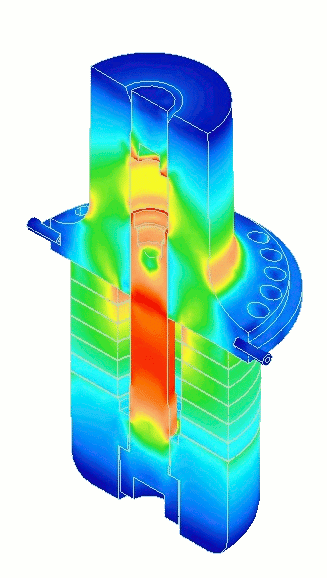
- Figure 3. Transducer performance (from FEA)
- Figure 4. Peripheral shell design
- Figure 5. 20 kHz transducer test for prestress
- Figure 5a. Transducer design
- Figure 5b. Damping resistance Z and frequency fs versus prestress T0
- Figure 6. Impedance versus current for various stack prestress
- Figure 7. Impedance at 300 ma
- Figure 8. Pressure distribution across transducer ceramics at back-driver/ceramic interface
- Figure 9. Effect of electric field strength on ceramic \( tan\delta \)
- Figure 10. Effect of electric field strength on ceramic permittivity
- Figure 11. Effect of static stress on \( d_{33} \)
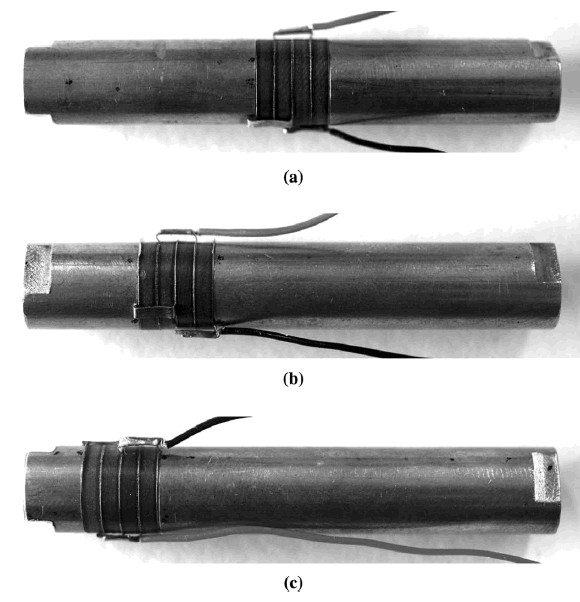
- Figure 12. Transducer with (a) centered ceramic, (b) moderate ceramic offset, (c) high ceramic offset
- Figure 13. Effect of ceramic offset on transducer amplitude
- Figure 14. Effect of ceramic length (shown in gray) and placement on \( \kappa_{eff}^2 \)
- Figure 16. Arrangement to measure ceramic voltages
- Figure 17. Ceramic voltage
- Figure 18. 120 kHz transducer cross section in area of ceramics
- Figure 19. Electrode with tangential wire
- Figure 20. Transducer with extended electrode disks
- Figure 21. Serpentine electrodes
- Figure 22. 55 kHz transducer — 6 ceramics, 2 serpentine electrodes
- Figure 23. Panel of photochemical etched electrodes
- Figure 24. Comparative machinability of frequently used stainless steels and their free-machining counterparts
- Figure 25. 20 kHz transducer with front driver wrench flats
- Figure 26. Effect of bolt on electromechanical coupling coefficient \( \kappa \)
- Figure 27. Transducer with Belleville springs (20) and radial cooling fins
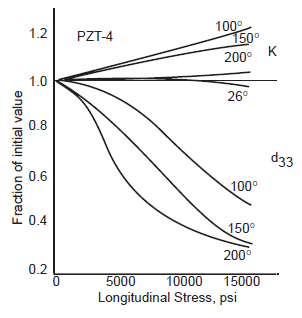
- Figure 28. Effect of temperature on \( \kappa \) and \( d_{33} \) for PZT-4
- Figure 29. 30 kHz transducer with arcing
- Figure 30. Metal welder prototype
- Figure 31. 30 kHz transducer with shifted ceramics
- Figure 32. 30 kHz transducer with cracked ceramics
- Figure 33. 15 kHz transducer power loading tests
- Figure 34. 15 kHz transducer power loading tests
- Figure 35. Arrangement for transducer electrical loading
- Figure 36. Effect of Curie temperature \( T_c \) on \( d_{33} \) for various ceramic compositions
- Figure 37. Full-wave transducer - ceramics in gray
- Figure 38. Kulicke & Soffa 80 kHz high power ribbon transducer
- Figure 39. Transducer with two stacks
- Figure 40. Two stacks driving a single horn (Herrmann Ultraschalltechnic)
- Figure 41. Radial transducer array
- Figure 42. 20 kHz transducer with rear inlet and exhaust cooling ports
- Figure 43. Half-wave transducer with radially finned cooling cylinders
- Figure 44. Full-wave transducer with intermediate radially finned cooling cylinder
Overview
Ultrasonic transducers transform electrical output from the power supply into vibrational output. This electormechanical transformation may be accomplished by piezoelectric ceramics (discussed here zzz) or magnetostrictive materials.
Transducer requirements will depend on the application. Many requirements will conflict with one another and will be given different priorities. Hence, no single set of guidelines can encompass all requirements — i.e., there are many different ways to achieve the same objectives.
Analytically, transducer performance can only be predicted in a general way. This is because the properties of piezoelectric ceramics are often highly dependent on the operating conditions including temperature, electrical field strength, static compressive prestress, dynamic stress, number of load cycles, and time. These operating conditions can interact with each other and the effects of these conditions are often nonlinear. Also, many properties of piezoelectric ceramics are orthotropic and can vary among the individual ceramics and also between ceramic lots. Further, the interactions at the various component interfaces (e.g., at threads) may be difficult to characterize and the coefficient of convective heat transfer may only be approximately estimated. Hence, much of the design process involves experimental testing.
(Note: see Mathieson (1) for a fairly extensive list of references.)
Langevin transducer
Almost all piezoelectric transducers for power ultrasonics are of the Langevin type -- i.e., one or more piezoelectric elements that are mechanically compressed (prestressed) between a front driver and a back driver.
The piezoelectric elements are typically constructed to operate in one of two modes: 33 or 31. See details.
33 mode
In the 33 mode the ceramic expands parallel to the applied electric field. The ceramics are disk shaped and pairs of ceramics are used (usually no more than three pair). This mode is most common (figures 1 and 2) and will be discussed below.
|
|
|
|
|
|
|
||||||||||
|
31 mode
In the 31 mode the ceramic expands perpendicular to the applied electric field. The ceramic is typically a tube with plating on the inside and outside diameters. Only a single ceramic is needed.
Prestress designs
Because ceramics are weak in tension, a static compressive prestress must be applied to prevent the ceramics from ever experiencing tensile stresses when the transducer vibrates ultrasonically. There are several arrangements for applying the prestress. The desired characteristics of the member that applies the prestress are discussed here. (In the literature, prestress may also be called preload or bias load.)
Center stack bolt
The center bolt design is the simplest, cheapest, and most common. This design is shown in figures 1, 2, and 2a.
Waanders (p. 49) recommends titanium for the stack bolt because of its high fatigue strength and low loss. However, steel bolts are most commonly used because they are readily available and relatively inexpensive. In addition, their fatigue stength easily exceeds that of titanium.
Stack stud with nut
This design is similar to the stack bolt but a stud is used instead. After the stud has been secured to the front driver, a nut is screwed onto the protruding section of the stud. The nut is then tightened against the back driver. This design is superior to the stack bolt in two respects:
- Whereas the stack bolt is a single material, the material for the stack stud and nut can be separately optimized. For example, the stud could be titanium (low stiffness for better electromechanical coupling) whereas the nut could be steel (high stiffness for more uniform ceramic prestress).
- The nut can be designed with a very large diameter. Then the face of the nut is relieved (recessed) except for a relatively small ring near the periphery. When this ring presses against the back driver, the resulting compressive prestress is more uniform than can be achieved by using a bolt with a relatively small contact diameter.
Integral stack stud
In some cases the stack stud may not be a separate component but, instead, is machined as an integral part of the front driver. This is common in medical transducers where fluid must flow through a central bore. This eliminates any possibe fluid leakage where the stack bolt would normally be threaded into the front driver and any chance that fluid contaminates might accummulate in this area. The disadvantage is that a large amount of front driver material must be machined away in order to create the integral stack stud. In addition, this is not suitable for an aluminum front driver since the resulting aluminum stack stud would not be strong enough to appply the required prestress to the ceramics.
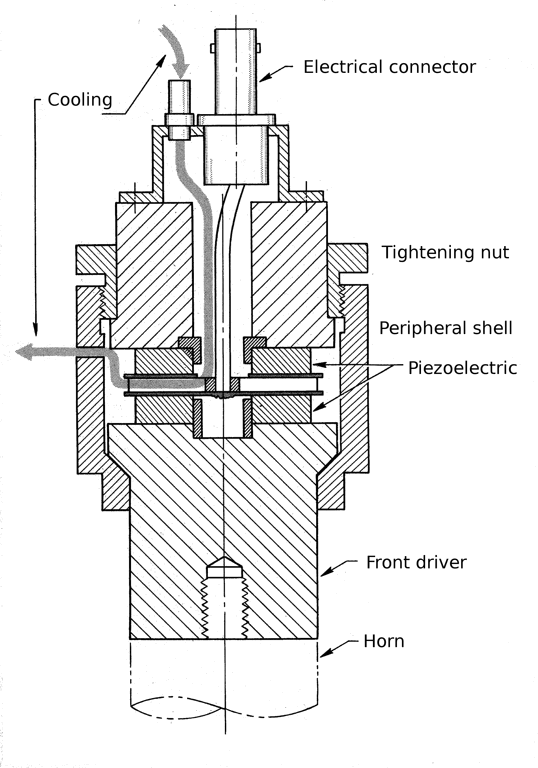
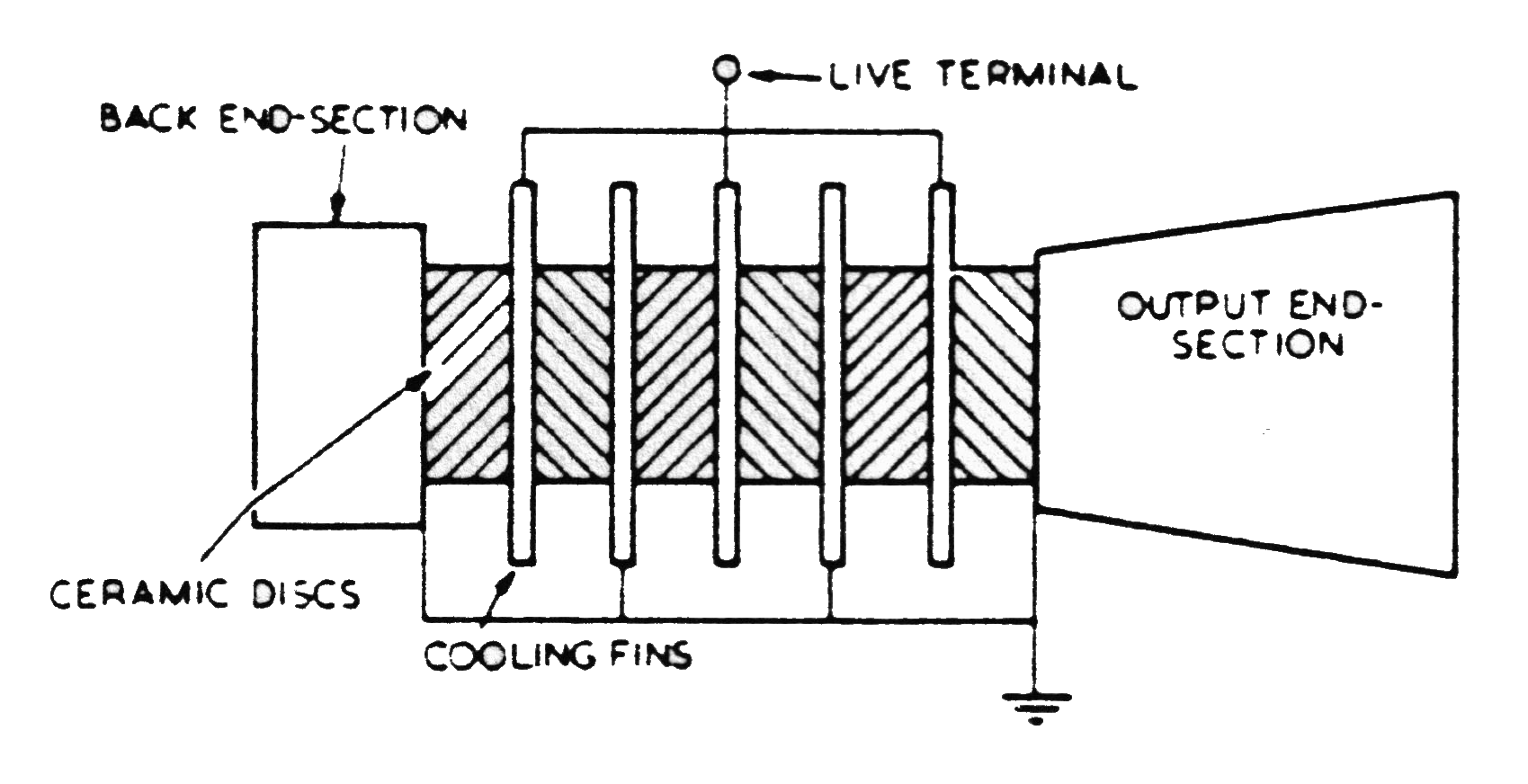
Peripheral shell
A peripheral shell is a cylinder that encloses the ceramics. For example, see Wave Energy Systems' transducer (figure 4).
|
|
|
In addition to prestressing the ceramics the shell can also serve as the transducer housing. Compared to the center bolt design, the peripheral shell has several advantages.
- Increased power —
- The ceramic volume can be larger since the ceramics don't need a central bore to accommodate the stack bolt.
- Because there is no need for a nodal flange to mount the housing, the ceramics can be centered at the transducer's node rather than being offset behind the nodal flange. This gives the highest electromechanical coupling between the electrical energy input and the vibrational output. Thus, the power can be twice that of a design where the ceramics are offset. (Wuchinich (0)).
- The prestress across the ceramics may be more uniform. Thus, the highest (peak) prestress at any location in the ceramics will be lower. This increases the allowed operating temperature. zzz --> better prestress = better resistance to flexure
- Better cooling (interior)
- Better resistance to flexure. With common center bolt designs the static prestress may be less than desired toward the ceramic periphery. Such designs may therefore be susceptible to ceramic damage due to flexure. By applying more uniform prestress the peripheral shell may reduce this problem.
- Better water tightness. Common center bolt designs support the housing with O-rings at the nodal flange. These O-rings are designed to isolate, rather than seal, the housing. If the nodal flange is not located at precisely the node then the flange will vibrate, thereby possibly allowing leakage. Since the peripheral shell design does not mount at a nodal flange, it can be more water tight. (Note: some center bolt designs use a rigid mount rather than O-rings at the nodal flange. Then the peripheral shell would not have a leakage advantage.)
- Better fatigue resistance. Since there is no stack bolt to be threaded into the front driver, there is no chance of front driver fatigue at that location. This might allow a material with lower fatigue strength. For example, magnesium might replace aluminum; since magnesium has significantly lower density (1740 kg/m3 versus 2810 kg/m3) the transducer's output amplitude would be correspondingly increased. Note, however, that the output threads where the stud is inserted might be unacceptably weak. Also, pure magnesium is highly flamable so care must be taken during machining. (Wave Energy Systems' design of figure 4 used a magnesium front driver. The reliability of this design is not known.)
- No arcing to bolt.
The disadvantages are the expense of the shell and nut; also, extracting the electrode leads may be difficult when there are more than two ceramics although this would be easier with serpentine electrodes. Active shell --> bad for hand held. Shell wall must be thin for max compliance. Assembly - concentricity of ceramic stack. Painting of ceramic ID if use interior cooling air.
For further information see Jones patent 3,283,182.
Peripheral stack bolts
This design is similar to the peripheral shell except that peripheral shell is replaced by a series of peripheral bolts. Like the peripheral shell, this design may provide more uniform prestress across the ceramics. However, the stack bolts must be tightened in a gradual criss-cross manner. If not done carefully this can lead to nonuniform ceramic prestress. In addition, the gradual tightening process means that the voltage across the tightening capacitor can bleed off, thereby giving an incorrect prestress reading. (See elsewhere.) Also, the peripheral bolts may introduce spurious resonances (Jones, p. 2) and may be slightly less efficient than center bolt/stud designs (APC International). Hence, this design is seldom used.
Determining the required prestress
The compressive prestress must be sufficient to prevent the ceramics from ever experiencing any ultrasonic tensile stress and to prevent any lateral ceramic slippage. The required prestress is not well defined.
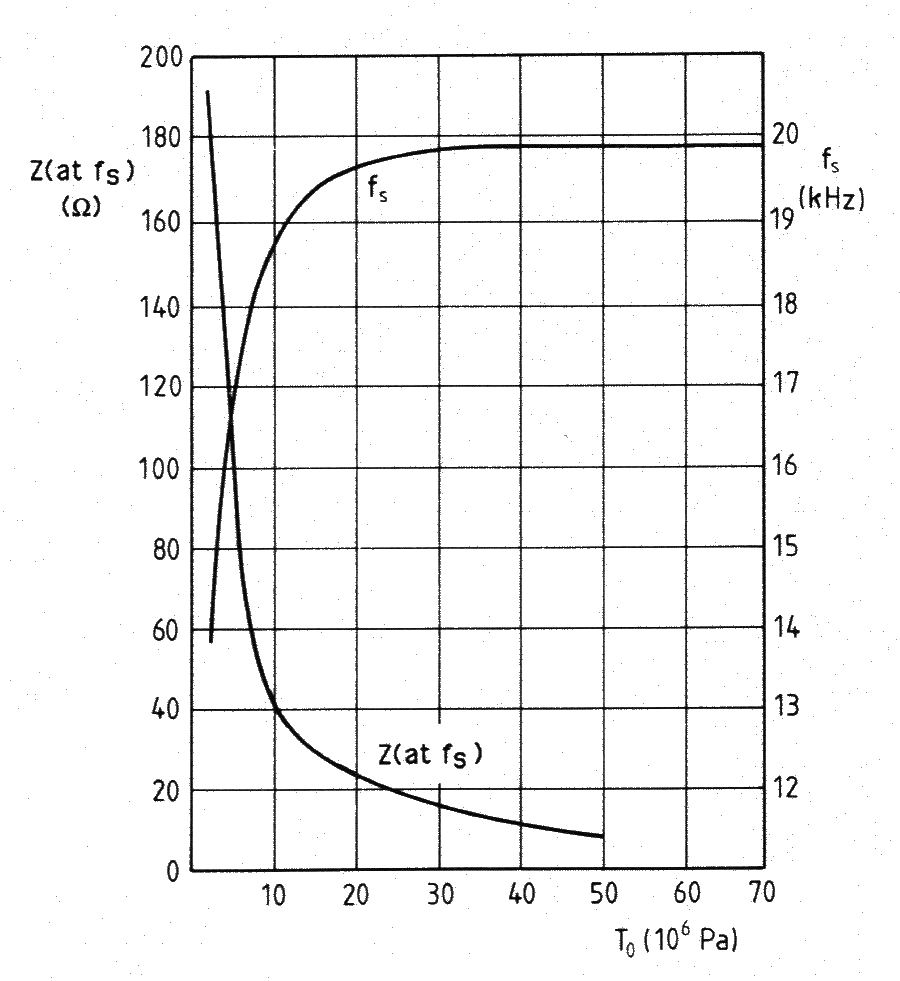
Hulst investigated prestress for the transducer shown in figure 5a. Figure 5b shows the change in damping resistance and resonant frequency with prestress for PZT4 ceramics. Hulst (p. 286) notes that the frequency has stabilized at about 35 MPa but even higher prestress is required to stabilize the damping resistance (~50 MPa from figure 5b). (Hulst states that the results were determined experimentally but the specifics are not given; in particular, it is not known if these results are from low-drive or high-drive tests.)
|
||||||||||
|
Since the resistance and frequency seem to stabilize with increasing prestress, why not just apply a very large prestress? Unfortunately, ceramic performance generally degrades as the prestress increases.
- "The dynamic \( d_{33} \) constant may decrease by about 30% if a prestress of 35 N/mm2 is applied to a stack of two disks. ... a similar behaviour is expected and found for g33." (Hulst, p. 290)
- "The properties of the ceramic are modified under compression-bias. In particular, the maximum safe temperataure at which the material will function efficiently may be drastically reduced." (Neppiras (3), p. 301) (This suggests that a high compressive stress may reduce the Curie temperature although specific confirmation has not been found.)
- "Excessive preload results in pronounced depoling, with unstable impedance and aging in operation." (DeAngelis (1), p. 1)
- "Compressive stresses may not exceed a specific limit as they could lead to mechanical depolarization, and strain mustn’t exceed a specific limit; otherwise, the mechanical losses of the ceramic will increase drastically, leading to heat-up and resulting in failure." (Lierke (1), p. 935)
Thus, a compromise intermediate prestress must be specified. This must be determined by actual tests of the particular transducer design. For example, DeAngelis (1) describes tests by which the optimum prestress was determined for 120 kHz wire bonding transducers. The tests were conducted on five transducers, each of which had a different prestress. All of the PZT8 ceramics were from the same production lot (aged for two years) and were verified for consistent performance prior to assembly. After assembly the ceramics were stabilized by heat treatment and cycling.
(Note: DeAngelis' tests used multiple transducers, one for each prestress level. However, for a center-bolt design a rough estimate of the effect of prestress might be determined with a single transducer by tightening the bolt in steps. However, this is not desirable because:
- The single stack of ceramics may not be statistically representative.
- Once a given prestress has been applied, the effect of any previous ceramic stabilization will be disturbed. Then the next prestress level will be affected by this disturbed stabilization. Attempts at re-stabilization will just confound the situation since the ceramics will not necessarily return to their previous stabilized performance.
In addition, the tests should be performed at high drive levels as the transducer will actually be used.)
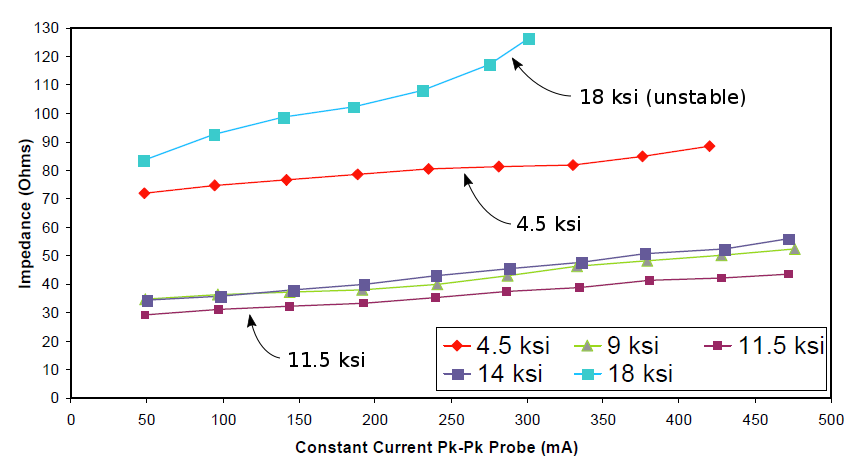
The tests of the assembled transducer included amplitude (via laser vibrometer), frequency, and impedance measurements. Impedance measurements (figure 6) seem to give the best discrimination among the various prestress levels. The X axis current correlates to the drive level (i.e., higher current indicates higher drive).
|
|
|
The 4.5 ksi prestress has high impedance because the ceramics are not adequately clamped whereas the 18 ksi prestress has high impedance because the ceramic performance degrades under excessive prestress.
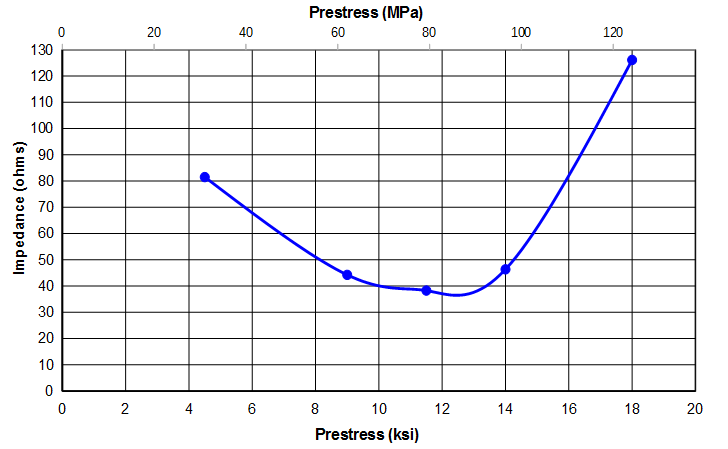
Figure 7 shows the above data at 300 ma (i.e., the highest current for which the 18 ksi data are available). For this particular transducer design a prestress between 9 kpsi (62 MPa) and 14 ksi (97 MPa) gives acceptably low impedance. In case the following may occur, an intermediate prestress within the acceptable range should be chosen in order to provide a factor of safety.
However, not all transducer designs may be this forgiving.
- Flexure or shock waves. An unbalanced horn (e.g., horns with face contours or bent probes) may send flexure waves back through the ceramics. Similarly, certain applications such as inserting may send shock waves back through the ceramics. Such waves may cause the ceramics to shift. The magnitude of these waves may not be predictable in advance. For example, a standardized transducer may be used with various boosters and various contoured horns whose degree of unbalance may not be known in advance.
- Thermal expansion. may reduce prestress. bolt vs ceramics
- Seating of ceramics and components.
|
|
|
The following prestress have been suggested or used; the assumed factors of safety are not known.
|
|||||||||||||||||||||||||||||||||||||||
|
Table notes:
- As noted elsewhere here zzz, PZT8 can sustain higher static stress than PZT4.
- The lower values of prestress are likely for "well behaved" systems (e.g., transducers with relatively uniform prestress across the ceramics and without flexure waves that may cause ceramic slippage or cracking) where a low factor of safety is acceptable. Hulst's design, where the loaded threads are far from the ceramics, should have fairly uniform ceramic prestress.
- "For PZT4 the maximum compressive stress should not exceed 15,000 psi [103 MPa] for static operation and 7,000 psi [48 MPa] for sustained cyclic operation." Channel Industries (1) (p. 4)
Prestress pressure uniformity
Prestress pressure uniformity over a specified ceramic surface is defined as:
\begin{align} \label{eq:10098a} \textsf{Prestress uniformity} = \frac {\textsf{Lowest compressive stress}}{\textsf{Highest compressive stress}}\end{align}
With a center stack bolt, the highest compressive stress typically occurs at the ceramic inside diameter while the lowest compressive stress typically occurs at the ceramic outside diameter. As the ceramic diameter increases in relation to its half-wavelength at the specified frequency, the stack bolt becomes less effective in applying a uniform prestress across the ceramic. Then the average prestress must be increased in order to maintain a certain minimum prestress at the ceramic outside diameter. However, this results in excessive at the ceramic inside diameter which can be detrimental to performance.
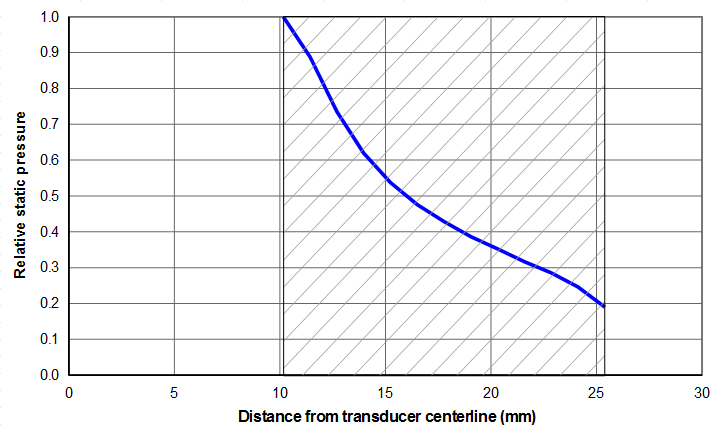
Figure 8 from Culp shows this effect for the transducer of figures 1 and 2. The ceramic in this transducer has an outside diameter of 50.8 mm and an inside diameter of 20.3 mm. These dimensions are shown by the hatch in the figure.
Figure 8 shows that the prestress uniformity is only 0.19 or 19%. When used with horns having some unbalance, this transducer was generally less stable than a similar design having ceramics with an outside diameter of 40.6 mm, possibly because the latter had substantially better prestress uniformity. (Note — the instability was exhibited as significantly higher temperatures in the ceramics and higher (unacceptable) loss compared to when running with a balanced horn.)
|
|
|
Factor of safety
The nominal prestress must be increased by a reasonable factor of safety in order to accommodate the following.
- Seating of the transducer components as the transducer is cycled. This may lead to reduced prestress.
- Different rates of thermal expansion among the transducer components (temperature rise due to normal power delivery, operation at high environmental temperature).
- Flexural waves due to resonator unbalance, off-axis loading, or interaction with secondary resonances. The nominal prestress is only designed to accommodate longitudinal vibration. If flexural waves are (or may be) present then additional prestress is needed to accommodate the associated flexural stresses.
- Shock (impact) loading. This may occur, for example, in inserting applictions.
- Nonuniform prestress pressure across the ceramic surface.
Applying the prestress
Thread & bolt head lubricants. Bolt unwinding. With stud can use hex wrench or similar to prevent the bolt from winding; otherwise, should account for winding when specify prestress.
Methods -- Torque; Ceramic voltage; Compression in hydraulic press (press alignment to apply uniform pressure to the ceramics)
Components
Typical components of a Langevin transducer are shown in figure 2. These are discussed below.
Piezoelectric ceramics
Piezoelectric ceramics are the heart of the transducer.
Types
Ceramics are typically classified as "soft" or "hard". Hard ceramics are used for power applications. Among hard ceramics there are two basic types, generally designated as PZT4 and PZT8. (PZT stands for lead-zirconate-titanate of which the ceramics are composed.) Different manufacturers may have their own designations for these types but the general performance is similar. The following table compares PZT4 and PZT8 at low field conditions.
|
||||||||||||||||||||||||||||||
|
Table notes:
- Values are at room temperature and low drive. Properties may be significantly different for high tempertures and/or high drive and should, therefore, not necessarily be used for design. ("It should be noted that at high drive levels QE and Qm0 can no longer be treated as constants - they are then often much lower than the low drive-level values." Waanders, section 6.1.1, p. 42)
- \( Q_m \) is measured for a thin disk.
- \( K^T_{33} \) is the ratio of the permittivity of the free (unclamped) ceramic to the permittivity of space.
- Except for the dielectric loss, higher values give better performance.
- Also see Berlincourt (2).
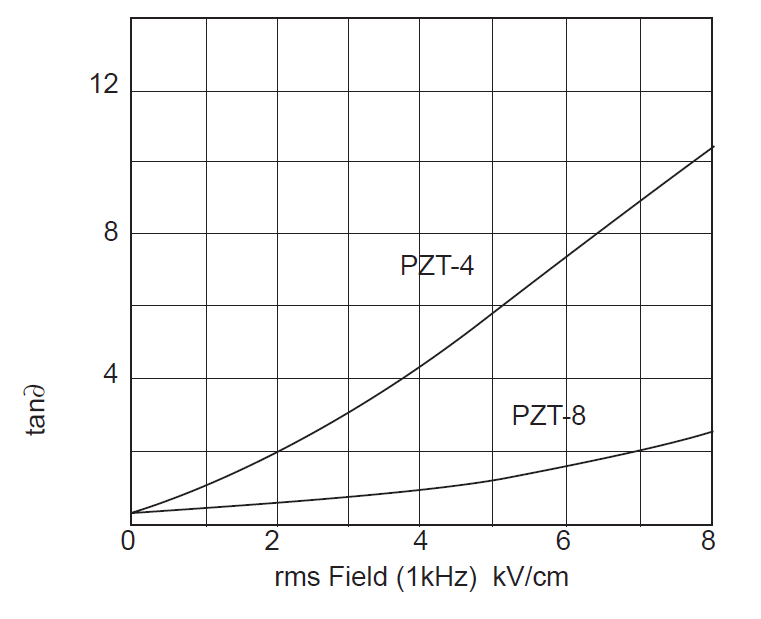
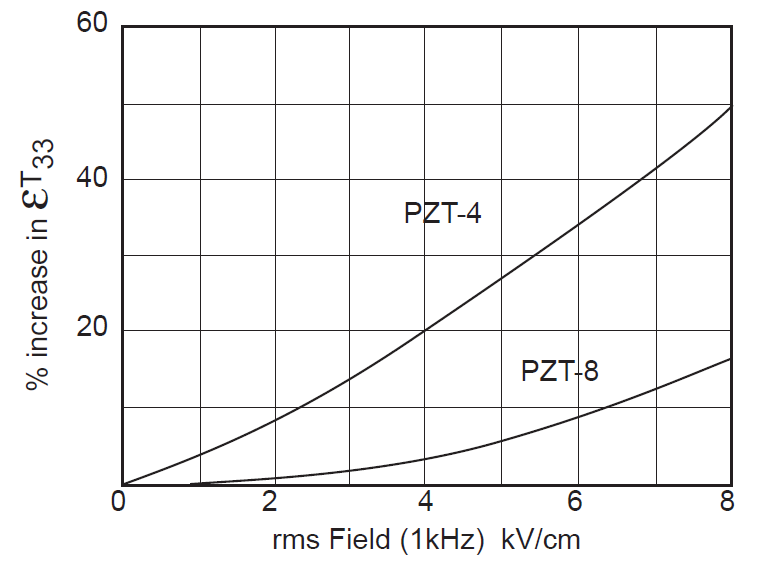
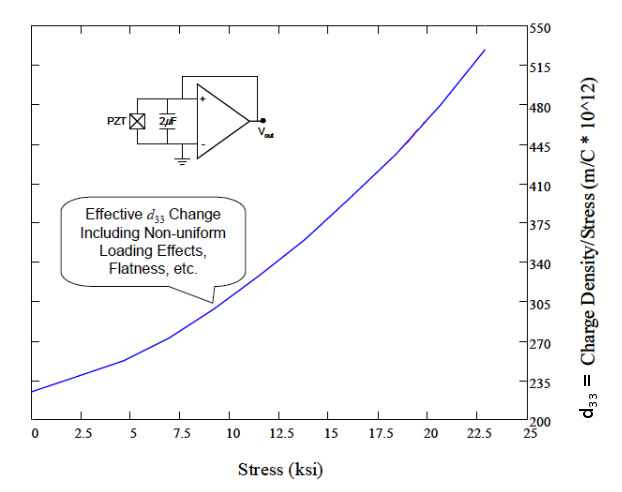
PZT401 has a higher strain constant \( d_{33} \) which will give higher amplitude and a slightly higher electromechanical coupling coefficient \( \kappa_{33} \). However, "PZT8 is recommended for applications requiring higher power handling capability than is suitable for PZT4." (Berlincourt (2), p. 2) Also, PZT8 is often less affected by the operating conditions than PZT4; for example, see figures 7 and 8.
zzz Morgan Technical Publication TP-226 lists max static compressive stress for PZT4 as 83 MPa
zzz "max static compressive stress" is the stress at which depoling occurs?
ZZZ As noted above, the maximum static prestress must be reduced if the transducer will be used under sustained dynamic operation (typical for power transducers).
Effect of operating conditions
Piezoelectric ceramics are often significantly affected by operating conditions. (See Berlincourt (1) for a fairly extensive discussion.) The following figures show examples for the electrical field strength and static stress. Also see the section on determining the prestress.
|
|
|
|
|
|
|
|
|
Figure notes —
- Figures 7 and 8 are from Berlincourt (2). The data were determined at room temperature without biasing stress. (See Morgan Technical Publication TP-217.)
- Figure 11 is from DeAngelis (1) (figure 9, p. 2). The static stress was applied uniformly across the ceramics with a tensile tester.
Placement
The piezoelectric ceramics are located between the back driver and front driver. Some minimum back driver stiffness is required in order to provide acceptable prestress across the ceramics; this stiffness depends on the back driver's length, material, diameter, and method by which the back driver is supported. The same considerations applies to the front driver.
In order to tune to the desired longitudinal resonance, the back driver and front driver lengths will often be longer than the minimum requirements. The question is, as the lengths of the back driver and/or front driver are adjusted, where should the ceramics be placed relative to the transducer's node? The ceramic placement should consider output amplitude, power delivery, loss, frequency stability, and mounting.
There are two basic placement possibilities: 1) the ceramic stack can be centered at the node or 2) the ceramic stack can be offset from the node.
Amplitude considerations
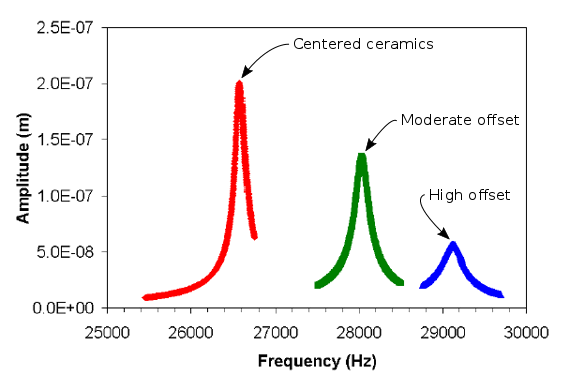
In theory, the transducer's amplitude will be maximized when the ceramics are located where the strain is highest (i.e., at the node); the amplitude will be reduced if the ceramics are moved away from the node. Mathieson's tests (figures 10 and 11) have verified this for a low drive level (one volt RMS).
|
|
|
|
|
|
(Note that as the ceramic offset increases the resonant frequency also increases. This is because the low-modulus ceramic material is effectively being replaced by higher-modulus front driver material (brass in this case), thereby stiffening the transducer.)
In order to maximize the output amplitude, the front driver's output diameter is often made smaller than the ceramic diameter. This is similar to building gain into boosters and horns. The amplitude will be maximized when the length of this reduced diameter is maximized. However, when the ceramics are centered the front driver length is shorter than with offset ceramics; this would reduce the amplitude somewhat compared to offset ceramics. Analysis would be needed to predict the net amplitude effect.
While centered ceramics give the highest amplitude at low drive levels, Mathieson shows that this may not be true at higher drive levels where nonlinear effects must be considered.
Power considerations
The approximate maximum power that a transducer can deliver is given by the following equation. (See the derivation and limitations.)
\begin{align} \label{eq:10070a} P &= 2 \pi f_s \, {E_3}^2 \, \varepsilon_{33}^T \, \kappa_{eff}^2 \, Q_M \, V \end{align}
where —
| \( P \) | = acoustic power delivered [W] |
| \( f_s \) | = series resonance frequency [Hz] |
| \( E_3 \) | = electric field strength [V/m] |
| \( \varepsilon_{33}^T \) | = piezoelectric permittivity at constant stress [(coulomb/volt)/m = Farad/m] |
| \( \kappa_{eff} \) | = electromechanical coupling factor [no units] |
| \( Q_M \) | = mechanical Q [no units] |
| \( V \) | = total ceramic volume [m3] |
With all other things being equal, the power will be maximized when the electromechanical coupling factor, the mechanical Q, and the total ceramic volume are maximized.
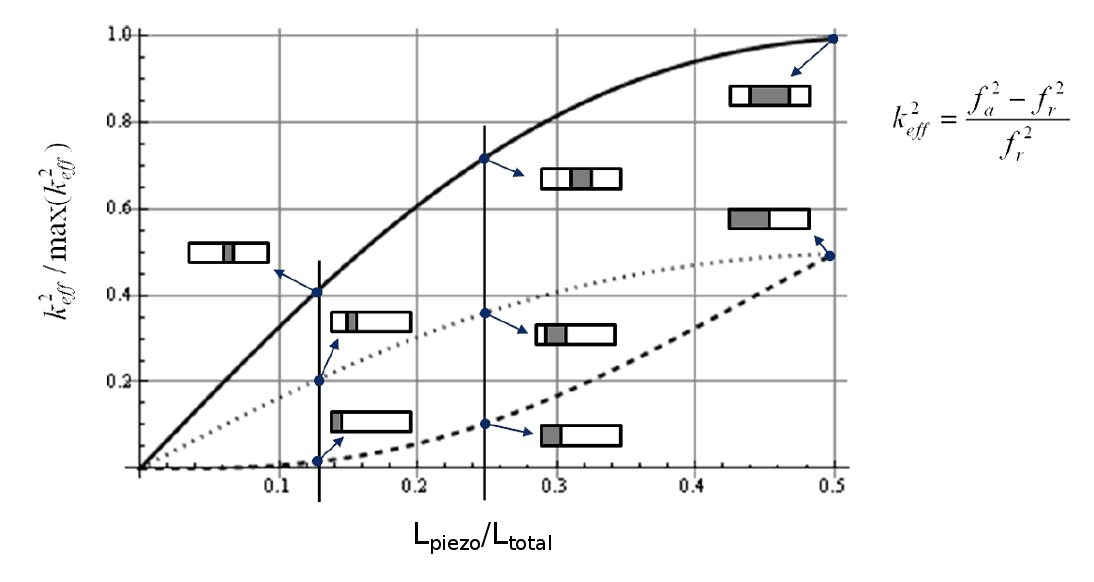
The effective electromechanical coupling coefficient \( \kappa_{eff} \) depends on the location of the ceramic relative to the node and on the ceramic volume. Figure 12 from Lierke (1) shows these effects.
|
|
|
where —
| \( L_{piezo} \) | = length of ceramic |
| \( L_{total} \) | = total transducer length |
| \( \kappa_{eff}^2 \) | = square of effective electromechanical coupling coefficient [no units] |
| max(\( \kappa_{eff}^2 \)) | = maximum possible \( \kappa_{eff}^2 \) for any of the considered transducer configurations [no units] |
As indicated in figure 14 —
\begin{align} \label{eq:10071a} \kappa_{eff}^2 &= \frac{{f_a}^2 - {f_r}^2}{{f_r}^2} \end{align}
where —
| \( f_a \) | = antiresonant frequency |
| \( f_r \) | = resonant frequency |
Notes —
- The ceramics are the gray area on each transducer sketch.
- The end masses (unshaded area) are the passive material — i.e., the same material as the ceramics except unpoled (no available piezoelectric effect).
- The transducer's cross-section is constant along its length.
- \( f_a \) and \( f_r \) can be fairly easily determined by FEA or the wave equation if the corresponding open circuit and short circuit moduli are specified.
Two conclusions can be drawn from figure 14 —
- Regardless of the ceramic placement, \( \kappa_{eff}^2 \) is maximized when the ceramic length is \( 1/2 \) of the transducer length (i.e., \( L_{piezo} / L_{total} \, = \, 0.5\)).
- For any given \( L_{piezo} / L_{total} \), \( \kappa_{eff}^2 \) is maximized when the ceramic is centered at the node (solid upper curve) where it experiences the maximum strain rather than being offset from the node (two lower curves) — the greater the offset the lower the \( \kappa_{eff}^2 \).
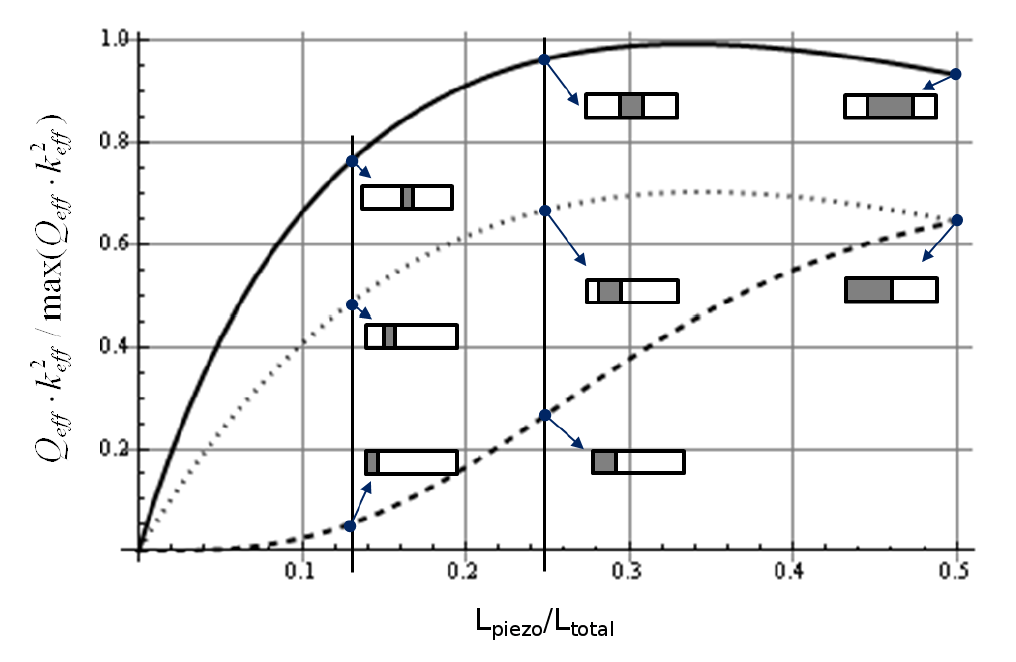
Lierke also considerd the combined effect of \( \kappa_{eff} \) and \( Q_M \) (figure 14x). As when considering \( \kappa_{eff}^2 \) alone, the optimum placement for the ceramics is again at the node (the upper curve). However, the optimum ceramic length is reduced from 0.5 to 0.33 (corresponding to the peak of the upper curve). In addition, note that the upper curve has relatively low curvature over a broad range. For example, the curve lies above 0.9 for \( L_{piezo}/L_{total} \) between 0.2 and 0.5. This means that the ceramic length is reasonably "near optimum" as long as it is greater than \( 0.2 \, * \, L_{total} \).
Assuming a wave speed in the ceramic of approximately 3200 m/sec (Waanders, p. 42), then \( L_{total} \) at 20 kHz would be 80 mm. Then the optimum ceramic length would be 0.33 * 80 mm = 26 mm and the "near optimum" length could range between 16 mm and 40 mm. (The 20 kHz transducer of figure 1 has six ceramics, each 5 mm thick, so the resulting \( L_{total} \) is 30 mm which is close to Lierke's predicted optimum.)
|
|
|
Although Lierke's analysis did not consider the effect of a load, he notes, "Almost the same behavior applies if the transducer acts against medium and strong loads, such as radiating into water or plastics welding." (p. 936)
Lierke's analysis appears to only consider the mechanical Q (related to the mechanical losses). However, under load the dielectric losses may substantially overwelm the mechanical losses.
Locating the ceramics away from the node (in an area of reduced strain) reduces the vibrational loss in the ceramics. However, this location may substantially reduce the available power (up to onehalf per Wuchinich (0)) due to reduced electromechanical coupling. (A patent by Shoh (1) suggests that the optimum location should be 1/12 wavelength from the free end of the back driver. However, this location is somewhat extreme and is seldom used.)
Loss considerations
Centered ceramic placement has two disadvantages. First, for an axially vibrating unshaped resonator the mechanical loss will be highest at the node (i.e., since the mechanical loss depends on the strain which is highest at the node). (This generalization excludes special considerations such as thread losses.) Since the inherent mechanical loss of piezoelectric ceramic is typically much greater than the loss of acoustic metals, this suggests that the tranducer's mechanical losses can be reduced by moving the lossiest material (the ceramics) away from the node.
However, when numerous offset ceramics are used, as in figure 1 and figure 2, those ceramics that are farthest from the node naturally experience lower strain than those closest to the node. (This is an acoustic requirement since the strain must eventually drop to zero at the antinode free ends.) To accommodate the reduced strain that occurs away from the node, the driving voltage should similarly decrease progressively away from the node. However, for design convenience all of the ceramics are typically driven at the same voltage.
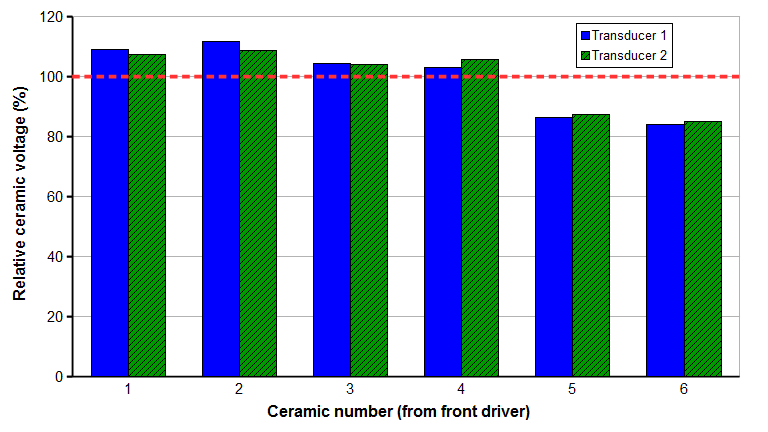
Culp (0) evaluated two test transducers like those of figures 1 and 2. In each case the test transducer was driven by a master transducer whose output amplitude was fixed. The induced voltage across each ceramic of the test transducer was measured in turn. Figure 16 shows the arrangement (after Hampton (1), p. 58).
|
|
|
Figure 17 shows the resulting voltages. The dashed line is the measured voltage when all of the ceramic pairs are connected in parallel; this is how the transducer would normally be operated so this is designated as the "normal" voltage. It turns out that the dashed line is also the average of all of the individual voltages for a particular transducer.
|
|
|
First, note from figure 3 that the node in the ceramics occurs approximately between the second and third ceramics from the front driver so this is the location of maximum ceramic strain. Comparing the highest and lowest voltages of figure 17, ceramic 2 is about 10% higher than the normal voltage whereas ceramic 6, which is farthest from the node, is about 10% lower than the normal voltage.
Notes —
- Both transducers were well aged (at least several years).
- No attempt was made to assure that every ceramic of a particular transducer had the same \( d_{33} \).
- Theoretically, the ceramic strain and induced voltage should decrease cosinusoidally from the node. The sudden voltage drop for ceramic 5 in both transducers is therefore interesting but currently unexplained.
As Roberts' patent 6,434,244‑B1 (2002) notes for such offset ceramic designs, "This [offset] leads to unwanted circulating currents, electrical losses, and unequal power contriutions for each pair of ceramic wafers."
Thus, the optimum ceramic placement (in terms of loss) seems unclear.
Mounting considerations
Centered ceramics are most common where no housing is required (e.g., for transducers used in cleaning tanks or, in some cases, where the support structure (e.g., the plastic welding stand) can serve as the housing). If a housing is needed then the centered design typically has a mounting disk that is centered within the ceramic stack. This can cause several problems.
- The electrode leads from the forward ceramics must be routed through or around this plate in order to attach to the rear electrical connector.
- The housing should be designed to prevent accidental contact between people or external objects and the high voltage ceramics or electrodes. This housing design can be somewhat awkward.
- If the housing must resist any static forces then these forces are transferred to the mounting disk and then directly to the adjoining ceramics. This potentially can damage the ceramics. This is mainly a problem for housings that are rigidly mounted to the transducer (less so for housings that are mounted with Orings).
Offset ceramics circumvent these problems since all of the ceramics are located behind the node. Then a separate mounting disk is not needed since the housing is attached in some manner directly to the front driver.
Mathieson (2) shows that ceramic placement can be used to suppress some unwanted transducer bending and torsional modes. However, this will not be effective for general purpose transducers (i.e., transducers that can accept a variety of boosters and/or horns). This is because the frequencies of the bending and torsional modes will change depending on the particular stack components that are added to the transducer. Thus, this approach will only be effective for a dedicated transducer (i.e., one that will only be used with a single booster and/or horn design) .)
Individual ceramic thickness
The ceramic thickness can't be arbitrarily chosen. "Optimising the thickness of the piezoceramic used within the stack of a Langevin transducer can be important [because] the thinner the piezoceramic element is, the better the electric field uniformity, the higher the effective electromechanical coupling coefficient and lower its impedance (higher the fow of current and hence amplitude for a given driving voltage). However, reducing the thickness of the piezoceramic element, increases the number of elements within the defined stack length which in turn increases the cost of manufacturing the transducer as well as increasing the capacitive value. Increasing the number of piezoceramic elements in the stack can also lead to inefficiency due to mechanical losses (caused through increasing the number of join interfaces) and drive problems, as too many elements can induce phase shifts among the elements causing them to counteract one another's oscillations. On the other hand thicker piezoceramic elements reduce the complexity of the transducer, hence reducing manufacturing cost as well as the mechanical losses (reduction in the number of join interfaces). However, thicker elements will also lead to a less uniform electric field at a given voltage whilst also increasing the impedance and internal heating [182-184]. Therefore a trade off between using many thinner piezoelectric elements and fewer thicker elements should be sought to achieve optimal performance." (Mathieson (1), pp. 53 - 54)
In addition, changing the number of ceramics will affect the transducer's capacitance. For example, consider a design where the ceramic thickness is halved while maintaining the total ceramic stack height. This doubles both the number of ceramics and the capacitance of each ceramic so that the total transducer capacitance increases by a factor of four. DeAngelis (2) (p. 1) notes that this may lead to drive problems.
To investigate the effect of ceramic thickness, DeAngelis (2) conducted a series of tests on 120 kHz wire bonding transducers using PZT8 ceramics. All ceramics were from the same powder and production lot. The transducers were subjected to stabilizing heat-treatment after build. Three ceramic thicknesses were evaluated but the total height of the ceramic stack was kept constant by adjusting the number of ceramics (figure 18).
|
|
|
The test transducers were driven at series resonance. At series resonance the impedance is low; thus, a relatively low voltage (but relatively high current) is needed to achieve the required power output. (Note: For parallel resonance the impedance is high so a high voltage is required. In order not to exceed the allowed ceramic field strength the ceramic thickness must therefore be limited. This thickness limitation may not be optimal for other performance parameters.)
Performance was evaluated based on zzz ...
As shown in figure 9, the dielectric loss (\( tan\delta \)) increases as the field strength increases.
Total ceramic thickness
Number of ceramics
Ideally, the number of ceramics would be the total ceramic thickness divided by the optimum ceramic thickness. If this yields an odd number then this is generally rounded to an even number so that the end surfaces of the ceramic stack that contact the front driver and back driver are both at ground potential.
If an odd number of ceramics is desired then one end of the ceramic stack would be at ground potential while the other would be "hot". This would result in a short through the stack bolt which connects the front driver and back driver. This problem can be avoided by placing an insulator at the interface of the "hot" ceramic surface and the mating driver surface. Macor® machinable ceramic has been used. Mylar might be possible.
Stabilization
The properties of piezoelectric ceramics will change ("age") with time. This will affect the transducer's performance. Hence, the ceramics should be stabilized (to the extent possible) before the transducer is shipped.
The initial stabilization simply allows the ceramics to age in an unstressed condition, typically for 100 days after poling. The ceramics can also be prestabilized by heating to about 200 °C for about an hour. (Berlincourt (1), p. 11) However, Morgan Electro Ceramics states that this process is normally only applied to PZT‑4. (Berlincourt (2), p. 1)
When the ceramics are assembled in a transducer, a new aging cycle begins when the prestress is applied. To accelerate this aging the transducer may be thermally cycled in an oven or may be cycled ultrasonically, often at somewhat overstress.
http://www.morgantechnicalceramics.com/sites/default/files/documents/chapter6b.pdf
Electrodes
Electrodes provide an electrical path from the power supply to the piezoelectric ceramics. For Langevin type transducers operating in the \( d_{33} \) mode, the electrodes are placed between adjacent ceramic disks. To the extent possible, the electrode material properties should be compatible with the ceramics in order to avoid unnecessary stresses. The following table compares the properties of electrode materials to ceramic materials.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Notes:
- Piezoelectric ceramic values depend on many factors including static stress, dynamic stress, electric field strength, and temperature. Young's modulus depends on whether the ceramic is at open circuit or short circuit condition. Also, piezoelectric ceramics are anisotropic. Therefore, the table values are approximate.
- Young's modulus for piezoelectric ceramics were taken as 1/compliance (i.e., 1/s33).
- The relative transverse mechanical strain \( \epsilon_t \) is the Poisson coupled transverse strain at 1 Pa axial stress (i.e., Poisson's ratio \( \nu \) / Young's modulus \( E \)).
- Electrode materials that are used by or suggested by —
- Nickel —
Branson Ultrasonics - half hard
Prokic (1) — 0.25 mm thick, 100 HV (Vickers ) - 140 HV (p. 6-3) - Beryllium copper —
Herrmann Ultraschalltechnic — "Copper-beryllium is used because it has high thermal and electrical conductivity. It is also strong and has high dimensional stability under thermal loading." (p. 18)
Waanders — 0.25 mm thick (p. 48) - Copper —
Hulst — very soft annealed (p. 285)
Neppiras (3) (p. 301)
Radmanović (p. 21) - Brass —
DeAngelis (2) (p. 4) - Invar —
Jones patent 3,283,182
Maropis (1), p. 133
- Nickel —
- http://www.morgantechnicalceramics.com/sites/default/files/documents/tp235.pdf suggests phosphor bronze or monel mesh bonded with resin. However, may not be able to plate phosphor bronze. zzz
- Note that Invar's coefficient of thermal expansion is comparable to that of the ceramic material. Thus, the ceramic should have little thermally induced stress from its contact with the Invar electrode. (Invar's fatigue strength is taken from Sokolowski.)
Design criteria
Under ideal conditions the following properties are preferred.
- As the ceramic expands laterally (due either to thermal expansion at the operating temperature or sterilizing temperature or due to Poisson coupling), stress will occur at the ceramic-electrode interface if the electrode does not naturally expand equally. In order to reduce these interface stresses:
- The electrode should have the same coefficient of thermal expansion as the ceramic.
- Poisson
- In order to accommodate mismatches in properties between the ceramics and electrodes, the electrodes should be as thin as possible. However, care must be taken that the unsupported portion of the electrode (that which extends beyond the ceramic-electrode interface) does not vibrate in undesirable ways which may lead to electrode fatigue.
- The electrode material must resist creep. Otherwise, the static prestress will be gradually released.
- The electrode's thermal conductivity should be high so that heat that is generated by the ceramics can be conducted away from the ceramics (e.g., into the front driver or back driver). However, this is not critical because the thermal conductivity of the ceramic is relatively low and the ceramic is much thicker than the electrode. Hence, the ceramic itself is the limiting factor in heat transfer.
In some designs the diameter of the electrode is made significantly larger than the ceramic diameter. The electrode's overhanging portion is exposed to the surrounding air so that heat that is conducted into the overhang will be convected into the air. In that case the electrode should be made thicker in order to aid the its conduction. (The effectiveness of this arrangement is not known. However, see the discussion of a similar design (Roberts patent 6,434,244‑B1, 2002) here.)
Prokic (1) (p. 6-3) states, "For electrode materials it is very important to use 99% nickel foils, or nickel-beryllium alloys, or some other nickel-rich alloys (which are relatively easy solderable, or where brazing can easily be applied, for creating good electrical contacts). Surface hardness of applied electrodes (empirically found as the best) should not be higher than 140 HV (Vickers) and not softer than 100 HV. Electrode-foil bands should be produced with cold drawing, without applying thermal treatment (resulting in relatively softer and more elastic alloys, with long fatigue-life). Electrode surfaces should be mirror and brilliant shiny, and extremely flat. Electrode thickness should be around 0.25mm. It is preferable not to apply any mechanical treatment on electrode surfaces (like polishing), because there is a danger to implement some hard particles in electrode surfaces (in any case, proper electrode cleaning should be applied in cases when any surface treatment is used)."
"The best materials for foil-electrodes of BLT are approx. 0.25mm thick foils, such as pure nickel (99%), or nickel, cooper, beryllium alloys (where nickel content is dominant). Material for production of foil electrodes should not be hardened (has to be very flat, very bright, to have almost mirror shiny surfaces, to be sufficiently soft and flexible, or half-hard, like in the case of elastic springs production: surface hardness between 100 HV and 140 HV is preferable). Foil electrodes could be produced using photo-chemical-etching technology to avoid formations of sharp edges. It is a common opinion that beryllium alloys are the best materials for contact electrodes of BLTs, but this is not correct, except if additional brilliant nickel plating, over such electrodes is applied (because beryllium itself is not sufficiently corrosion resistant, it has relatively high surface-friction coefficient, and under strong planar-radial vibrations starts degrading, separating cooper from beryllium)." Prokic (1) (p. 6-6)
Electrode arrangements
There are three common electrode arrangements.
Disk with a tab extension
For a transducer with N ceramics, there are typically N electrodes (sometimes N+1), each with its own wire. All of the positive electrodes are tied together electrically by their individual electrode wires; similarly for the ground electrodes. The tab may have a hole through which the wire passes to additionally secure the wire.
Depending on the materials, the wires can be attached by soldering, brazing, or welding (e.g., by resistance or electron beam). Soldering can be done before assembly (provided that the solder is kept clear of the eventual ceramic-electrode interface area) or after assembly. Brazing and welding must be done before the stack is assembled; otherwise, the ceramic may overheat locally near the braze or weld. Each wire is typically attached so that it aligns tangentially to the electrode periphery and generally in the same plane as the electrode. (However, see below.)
|
|
|
Attaching the wires very close to the ceramics allows a smaller transducer diameter. However, the wire will then vibrate with approximately the same amplitude as the ceramic. This may cause the wire to fatigue (typically where it attaches to the tab).
If a longer tab is used then the tab length must be tuned to provide minimum vibration amplitude. The wire is then attached at the tab's flexural node which reduces the liklihood that the wire will fatigue. This may require a larger diameter housing to accommodate the tabs.
Extended disk
Figure 20 (Neppiras (3), p. 300) shows a transducer with extended electrode disks where the diameter of the electrode is significantly larger than the ceramic diameter in order to aid heat transfer. Heat is conducted into the overhanging portion and is then is convected into the surrounding air (or liquid coolant). In this case the electrode should be made thicker than usual in order to aid the conduction. (The effectiveness of this arrangement is not known. However, see the discussion of a similar design (Roberts patent 6,434,244‑B1, 2002) here.)
|
|
|
Serpentine arrangement
This arrangement uses only two pieces of electrode material, regardless of the number of ceramics. Here, the electrode disks are connected between ceramic surfaces of like polarity by a narrow strip of the same electrode sheet (i.e., one electrode snakes between the positive ceramic surfaces while the other snakes between the negative ceramic surfaces).
|
|
|
|
|
|
This design has several advantages over the tabbed disk:
- Depending on the design, the strip that joins the electrodes may protrude less than a tab. Hence, the transducer diameter can be smaller. This may be especially desirable for hand-held medical transducers.
- Regardless of the number of ceramics, only two electrodes are needed. Hence, only two terminating wires are needed for the external connection.
- Compared to tabbed electrodes whose wires are attached prior to assembly to the transducer, there is no possibility of contaminates (solder, flux, etc.) on the electrode contacting interface.
One disadvantage is that the electrode must be precisely bent into shape prior to assembly. Also, the serpentine shape makes the stack alignment more difficult so an alignment fixture is highly recommended.
Fatigue
The protruding portion of the electrode will vibrate, typically at the operating frequency of the stack. This vibration can be minimized by proper design and/or by damping the vibration (e.g., by applying a silicone RTV to the overhang).
Note that the fatigue strength generally increases with the material's hardness. However, if the electrode material is too hard then it may not conform as well to small irregularities in the surface of the ceramic. Therefore, a half hard condition has generally been specified. This is less critical if the ceramic and/or electrode have been plated with a compliant material (e.g., silver, gold).
Plating
It may be desirable to plate the electrode with the same material as the plating on the ceramic. This serves two purposes.
- The plating can fill small imperfections between the electrode and ceramic. This allows better coupling between the electrode and ceramic and lower loss. (See Branson patent 3,066,232.)
- Due to the static prestress, ultrasonic vibration, and temperature rise, the ceramics and electrodes may join together by diffusion bonding to create a monolithic stack. This eliminates the possibility that individual ceramics will slip laterally when excited ultrasonically. This may also provide better coupling and lower loss.
During the plating process plating may build up around sharp corners (e.g., at the outside and inside diameters). Then the electrode will not be flat and may not couple well to the ceramics. Hence, the electrodes may need to be polished or lapped after plating in order to remove this buildup. This also applies to plating on the ceramics. ZZZ
Plating thickness ZZZ
Manufacturing
Electrodes should preferably be manufactured by photochemical etching. This assures that there are no imperfections (burrs, etc.) that might interfere with contact with the ceramics.
|
|
|
Back (rear) driver
The back driver distributes compressive prestress across the ceramics.
Materials
The following table shows the properties of common or suggested back driver materials.
|
||||||||||||||||||||||||||||||||||||
|
Table notes:
- Other stainless steels will have properties similar to 416 stainless.
- Plansee Densimet® D176 (93% tungsten, 5% nickel, 2.5% iron) was chosen because because of its relatively high machinability (compared to pure tungsten). There is also some fatigue data for this alloy (López and Paez, figure 5.15, p. 56). However, other tungsten alloys may be equally suitable.
Compared to aluminum or titanium, steel has several advantages.
- Better prestress. Because steel has a higher Young's modulus, it is stiffer and hence the prestress will be applied more evenly across each ceramic.
- Shorter transducer. Because steel is denser the back driver will be shorter so the overall transducer can be somewhat shorter. (Note: shortening the back driver reduces its axial stiffness. Therefore, this somewhat offsets the above prestress advantage compared to if an equal volume of steel could have been directly substituted for aluminum or titanium.)
- Shorter stack bolt. Because the back driver is shorter the stack bolt can also be shorter. This may be helpful in dealing with flexure resonances in the stack bolt (i.e., a shorter stack bolt will shift the flexure resonances higher). Note, however, that a shorter bolt is not always beneficial. zzz
- Shifted secondary resonances. Because of its shorter length, the secondary resonances will shift. This shift could either be helpful or harmful, depending on exactly how these secondary resonances shift in relation to the primary resonance and to other secondary resonances.
- Reduced rear driver amplitude. Because of steel's greater density and modulus, the rear driver will have reduced amplitude. If the rear driver is exposed to a liquid (e.g., for cooling) then the lower amplitude will reduce the acoustic energy that is undesirably transmitted into the liquid.
Among steels stainless is preferred because of its corrosion resistance. Any grade of stainless should be suitable but 416 offers superior machinability. 303 stainless and 316L (Branson Ultrasonics) are also used.
|
|
|
Tungsten alloys further maximize the above advantages. Radmanović (pp. 142 ‑ 144) used a 92W‑4Ni‑4Fe back driver for a 26 kHz transducer. Compared to a steel back driver, the back driver length decreased from 31.5 mm to 12.0 mm and the bandwidth increased somewhat. Tungsten alloy back drivers have also been used in sonar transducers.
The main disadvantage of steel is its relatively low thermal conductivity (25 W/m-°K) so heat will be conducted relatively slowly from the ceramics. Tungsten is about three times better while brass and aluminum are about five times better. Brass might be preferred to aluminum because its higher Young's modulus would give more uniform prestress across the ceramics. However, an aluminum back back would be longer so its increased surface area would aid in convective heat transfer. (See the section on cooling.)
Because the back driver is located near an antinode (where the strain is low), the resulting back driver loss is also low, regardless of the material. Hence, although both steel and tungsten (Mathieson (1), p. 58) have higher loss than either aluminum or titanium, they may be used as back drivers without concern.
Effect on output amplitude
Assume an idealized transducer where all static and dynamic stresses across any cross-section are planar. If the strain in the ceramics is maintained at a specified level then the chosen back driver material will only affect the back driver's amplitude, not the front driver's output amplitude.
In actual practice, however, the stress will not be planar but will be lower toward the periphery of the ceramics, particularly when the ceramic diameter is large. Then, substituting a stiffer material such as steel or tungsten will give more uniform stress across each ceramic. This might more effectively utilize the piezoelectric properties of the ceramics which could, in turn, increase the amplitude of both the back driver and front driver. zzz What if the ceramics aren't centered at the node?
This could be modeled by finite element analysis where each ceramic would consist of a series of concentric mating rings. Then the piezoelectric properties each ring would be adjusted according to the ring's static and dynamic stresses.
Shape
The back driver is typically a cylinder with the exposed end surface parallel to the ceramic surfaces. However, Puskas (1) (pp. 5, 6) indicates that adding a significant bevel at the rear of the back driver can flatten the impedance curve, thereby increasing the transducer's bandwidth. The effect on other performance parameters is not known.
Dimensions
The back driver must be sufficiently thick (stiff) to apply reasonably uniform prestress across the ceramic stack. When the stack bolt is a socket head cap screw, a rough rule of thumb is that the thickness of a steel back driver should be at least 45% of the ceramic diameter. For other back driver materials, the minimum thickness can be adjusted roughly inversely to their Young's modulus. For example, Young's modulus for aluminum is approximately 1/3 that of steel so the minimum back driver length should be three times greater than steel.
(The above thickness assumes that the stack bolt is a standard socket head cap screw which has a limited head diameter. If the socket head cap screw is replaced by a bolt with a larger head or a stud with a large diameter nut then the prestress will more uniformly distributed radially across the ceramic (i.e., better stress at the perphery). Then a thinner back driver could be used.)
The back driver's diameter must be at least as large as the ceramic diameter. However, an even larger diameter may be beneficial. Why? See zzz
The back driver may be counterbored for the stack bolt head, either to reduce the transducer's overall length or to allow a standard length stack bolt to be used. However, counterboring will somewhat reduce the uniformity of the prestress across the ceramics.
Front driver
The front driver delivers the transducer's ultrasonic energy to the booster, horn, or probe. The front driver often includes a mounting flange for attaching a housing and may include cooling holes for forced air cooling. (See cooling.)
Excluding transducers for cleaning tanks, the front driver will have a means (typically wrench flats or spanner holes) for tightening to the booster or probe. Although spanner holes may be less expensive to machine, wrench flats are preferred because they will have less wear from wrenching. Also, spanner holes may not be suitable for small diameter front drivers (e.g., for surgical transducers).
|
|
|
Materials
Compared the the back driver, the front driver material will often be less dense in order to give the maximum output amplitude (due to conservation of linear momentum across the node). The following table shows the properties of common or suggested front driver materials. (The properties of stainless steel (a common back driver material) and PZT ceramics are also included for comparison.)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Titanium
The table shows that titanium has high yield strength and high fatigue strength. However, it has relatively poor thermal conductivity so it will not be able to conduct ceramic heat well.
Aluminum
Aluminum has relatively low density (for highest amplitude) and good thermal conductivity. A disadvantage of aluminum (and also magnesium) is that the front threads (where the booster or horn stud engages) may wear more quickly from repeated tightening. Therefore, some designs incorporate a stud that is permanently installed in the front driver rather than in the mating booster.
Magnesium
Magnesium (suggested by Waanders, p. 44) has the lowest density of the listed materials and will therefore yield the highest amplitude. However, its thermal conductivity is inferior to aluminum. It also has the lowest yield strength and fatigue strength. Both of these strength problems can be mitigated by using a full length stack bolt that screws into a nut that is recessed in the face of the front driver. The stack bolt would then extend beyond the face of the front driver to allow a booster or horn to be attached. However, the extra length of the stack bolt may introduce unwanted stack bolt modes.
Multi-material
Compared to titanium, aluminum and magnesium have relatively low fatigue strength. This may lead to fatigue failures, particularly in the threads where the stack bolt engages the front driver. On the other hand, these materials have low density so the output amplitude can be higher than with titanium. These materials also have better thermal conductivity. A compromise is to use a two-part front driver — e.g., an aluminum base section (a washer whose outside diameter may be contoured) that mates to the ceramics and a following titanium nose output section. The stack bolt passes through a clearance hole in the base section and engages the threads in the titanium nose section, thereby compressing the base section between the ceramics and nose section. This approach avoids possible thread fatigue failure in the base section while still retaining the benefits of the aluminum or magnesium base section. The material and machining costs may also be lower than using an all-titanium front driver. This will require a longer stack bolt which may or may not be beneficial. This is the design that Branson used for their 10 kHz metal welders.
In addition, the front driver length can be reduced which may be an advantage in certain circumstances (e.g., for shorter medical handpieces). This happens when the base section has a low modulus (e.g., aluminum) and the nose section has a high density (e.g., titanium or steel). Since the resulting front driver is less stiff than if it had been made from the nose material alone, the front driver length must be reduced in order for the transducer to tune.
Plating
Aluminum and magnesium are normally plated, either for appearance or corrosion resistance. Platings include anodize, soft nickel, and chrome.
Thread engagement (center bolt design)
Thread engagement should be sufficient to prevent stripping of either the bolt threads or front driver threads. Thread engagement should not be excessive because the threads may be a significant source of power loss, especially if the threads are near the node.
Stack bolt
The following specifically addresses a transducer with a center stack bolt but is applicable to any member that applies prestress to the ceramics.
Desired characteristics
Low axial stiffness
The electromechanical coupling \( \kappa_2 \) will be maximized when the bolt has a low stiffness compared to the ceramics, thereby allowing the ceramics to expand relatively freely without being impeded by the bolt. Low bolt stiffness can be achieved by using a long bolt and by reducing the bolt diameter in the shank (non-threaded) area. (For example, see the transducer of figure 5a. By using a bolt with a reduced shank diameter, the thread diameter can remain large in order to absorb the bolt's prestress tension load.) Bolt stiffness can also be reduced by using a material with lower Young's modulus (e.g., titanium or beryllium copper instead of steel).
These conclusions can be seen from the equation for the adjusted coupling coefficient \( \kappa_2 \) —
\begin{align} \label{eq:10099a} {\kappa_2} &= \frac{1} { \sqrt{ \left({\Large\frac{1}{{\kappa_1}^2}} -1 \right) \left({\Large\frac{Y_b \, A_b \, / \, L_b}{Y_c \, A_c \, / \, (n \, L_c)}} +1\right) +1 } } \end{align}
where —
| \( \kappa_2 \) | = electromechanical coupling coefficient with the stack bolt |
| \( \kappa_1 \) | = electromechanical coupling coefficient without the stack bolt |
| \( Y_b \) | = Young's modulus of bolt |
| \( A_b \) | = cross-sectional area of bolt shank |
| \( L_b \) | = free length of bolt shank |
| \( Y_c \) | = Young's modulus of ceramic |
| \( A_c \) | = cross-sectional area of ceramic (i.e., the area of the individual ceramic's flat face) |
| \( L_c \) | = length (height) of individual ceramic |
| \( n \) | = number of ceramics |
The derivation of the above equation shows that \( \kappa_1 \) depends only on properties of the ceramic, not on the number of ceramics or other parameters —
\begin{align} \label{eq:10099b} {\kappa_1}^2 &= \frac{1}{{\left(\Large\frac{\varepsilon}{Y}\right) } \left(\Large\frac{1}{d_{33}} \right)^2 +1} \end{align}
where —
| \( E \) | = electric field strength [v/m] |
| \( \varepsilon \) | = ceramic permittivity [v/m] |
| \( d_{33} \) | = piezoelectric strain constant [m/v] charge constant [Coulonb/N] |
Equation \eqref{eq:10099a} shows that as the area of the bolt goes to zero (i.e., no bolt), the adjusted electromechanical coupling coefficient \( \kappa_2 \) just converges to the unadjusted electromechanical coupling coefficient \( \kappa_1 \). In practice, of course, the bolt must retain sufficient area to apply and maintain the required prestress on the ceramics.
Note: Equation \eqref{eq:10099a} applies when the displacements in the ceramic and the adjacent bolt section are equal. Under static conditions this will occur when the ceramic and bolt are simultaneously compressed between rigid anvils. In general this will not be precisely true for dynamic operation. Nonetheless, equation \eqref{eq:10099a} would still indicate the general trend. See further discussion of the electromechanical coupling coefficient.
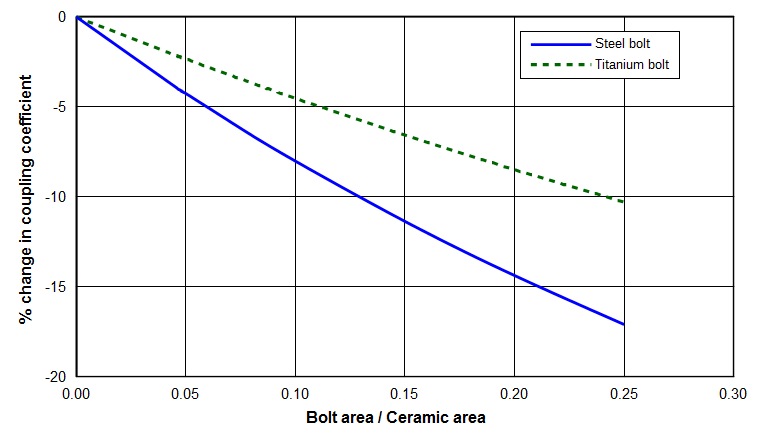
Figure 26 shows the effect of bolt area on the coupling coefficient.
|
|
|
Consider the transducer of figure 1. The stack bolt has a diameter of 12.7 mm (area = 127 mm2) and the ceramic has an outside diameter of 50.8 mm and an inside diameter of 20.3 mm (net area = 1703 mm2). The ratio of bolt area to ceramic area is then 0.074. From figure 26, the presence of a steel bolt reduces the coupling coefficient by 6.1% compared to a transducer without a bolt. Some other stack bolt parameters are shown in the following table. Note that a Ø12.7 mm steel bolt is three times worse than a Ø9.5 mm titanium bolt (2.0% reduction). Practically, however, this requires that the Ø9.5 mm titanium bolt should be able to resist the associated static and ultrasonic stresses. Of course, a titanium bolt would be more expensive than a steel bolt so the improved performance with titanium might not be cost effective.
|
|||||||||||||||
|
Compatible front driver stiffness
The front driver stretches as the transducer vibrates; likewise the bolt threads also stretch. However, when the front driver material and bolt material are not the same, the preferred amount of stretch for each is not the same. For example, the threads of a steel bolt would tend to stretch only 1/3 as much as the mating internal threads of an aluminum front driver because steel's Young's modulus is three times higher. This incompatiblity can cause heating where the threads mate due to sliding friction; it can also cause undesirable stress in the front driver threads which can lead to front driver fatigue failures. This problem can be reduced by using a bolt material with lower Young's modulus (e.g., titanium) or by counterboring the bolt in the threaded area in order to reduce its stiffness (as is done by Branson for their 500/900 series transducers).
Compatible coefficient of thermal expansion
When the transducer operates at high temperature (either due to losses during high power delivery or due a high temperature environment), the stack bolt and ceramics will expand. The ceramics have a very low coefficient of thermal expansion (typically ~1.7 x 10-6/°C). The comparative values for titanium and carbon steel bolts are 8.6 x 10-6/°C and 12.3 x 10-6/°C, respectively. (The material for the referenced steel bolt is 4140, taken from Unbrako, p. 70.)
Note that the actual expansion of each component also depends on its temperature. Because most of the heat is generated within the ceramics, their temperature will be higher than the bolt. Thus, the difference in expansion between the ceramics and bolt will not be as great as might be assumed from their coefficients of thermal expansion alone. None-the-less, the bolt will likely expand more than the ceramics so the the room temperature compressive prestress on the ceramics will be at least somewhat reduced. This will be especially true under a high duty cycle where the temperature throughout the transducer stack will tend to equalize.
To counteract this problem, Scarpa (p. 10; claim 15, p. 15) used Belleville springs under the bolt head (figure 27). If properly designed, such springs can apply a constant force over a relatively wide range of deflections. Thus, even when the stack bolt expands, the washers will continue to apply a uniform preload to the ceramics. In order to provide sufficient preload force while being limited to the diameter of the back driver, multiple stacked washers may be needed. This arrangement (even with a single washer) may generate excessive frictional heat at the washer interfaces.
|
|
|
High fatigue strength
In addition to the ultrasonic stress, the bolt will have high static stress due to the ceramic preload. This high tensile stress will reduce the allowed ultrasonic stress in the bolt (for example, according to the Goodman or Gerber failure relations). zzz give example. Thus, the nominal (unloaded) fatigue strength must be high in order to accommodate the added static prestress.
High yield strength
A high strength material allows a smaller bolt diameter for a given static prestress load. A a smaller bolt diameter permits a smaller ceramic inside diameter. Thus, more ceramic can be used if the ceramic outside diameter is maintained or a smaller ceramic outside diameter if the same volume of ceramic is maintained. A smaller diameter bolt also increases the electromechanical coupling (above).
Optimum material
Ignoring costs, titanium (such as Ti-6Al-4V) best meets the above requirements. To reduce the material and machining cost, a titanium stud (without bolt head) could be mated to a steel nut at the back driver.
Length
Ideally the stack bolt should be as long as possible. This has two advantages.
- Improved electromechanical coupling. A long stack bolt reduces the stack bolt stiffness relative to the ceramics. (The best condition would be a bolt with zero stiffness. See above.)
- More uniform ceramic prestress. With a long bolt the point of application of the prestress force is farther from the ceramics. This gives a more uniform prestress across the ceramic diameter. This is more important for larger diameter ceramics where the periphery of the ceramics may be poorly supported.
Unfortunately, one problem with long bolts is that they are more likely to have undesirable secondary (flexural or longitudinal) modes near the primary mode. Such modes can cause high loss, damage to the ceramics or front driver, or bolt fatigue failure. DeAngelis (p. 20) recommends a 10% frequency separation for dry stacks and 20% separation for glued stacks.
If the bolt is sufficiently long then it can thread into the front of the front driver. In this antinode region the strain is low so the risk of fatigue failure is reduced. The threaded end of the bolt can even extend beyond the end of the front driver (i.e., as a replacement for the stud) so that a booster or probe can be attached. (See the design of Hulst, figure 5a.) For this design the bolt must be secured tightly to the front driver (e.g., by suitable thread lock) so that it can't loosen when the booster is tightened. Stud with nut preferred. zzz
If loc-tited, can't retorque.
If the bolt is exactly designed (per Hulst) then the bolt will have the same resonance as the transducer and will not impose any additional stress on the transducer.
Note: Hampton - bolt should be stretched at least 10x the expected amplitude.
Head diameter
The head diameter should be an appreciable percentage of the ceramic diameter. Flared head; undercut.
Threads
From available thread pitches for a given bolt diameter, a fine pitch is generally preferred.
Electrical insulation
The ceramics must be protected against electrical arcing and also against moisture (which can contribute to arcing). Therefore, a conformal coating is applied to the exposed ceramic and electrode surfaces. This must be done after assembly so that the resulting coating is uninterrupted (i.e., all gaps, particularly between ceramics and electrodes are completely sealed).
In addition to high electrical and moisture resistance, the coating should have low loss when vibrated ultrasonically. Thus, the coating thickness should be small. Also, the coating should retain its properties at the expected ceramic operating temperatures. Numerous coatings have been used including magnet wire lacquers (e.g., Conap), silicone spray. The following coatings have been suggested by Piezekinetics.
Some coatings such as Conap may take several days to cure completely. During this time the ultrasonic loss will decrease. Therefore, loss tests should not be conducted during this time.
One problem with a center bolt design is that the interior ceramic and electrode surfaces can not be conveniently coated after assembly. However, monolithic ... ; problem with moisture if center cooling.
Electrical isolation
In some cases the piezoelectric stack must be electrically isolated form the rest of the transducer. In this case a thin insulator disk can be placed between the front driver and ceramic stack and also between the back driver and the ceramic stack. Macor® (a machinable ceramic) is commonly used. Mylar washers can also be considered.
Mechanical fits
All parts of the transducer must be carefully processed or machined to assure proper fits. This will assure that mechanical frictional losses are minimized and that maximum energy it transferred to the load.
Stack bolt threads
The stack bolt threads into the front driver. Two investigators indicate that properly machined and mated threads are important.
- Neppias — "The [transducer's] mechanical resistance, R*, is made up from: internal material-loss; losses at the contacting surfaces; and frictional damping in the screw-threads. The last named is by far the most important." (p. 298 )
"Dynamic frictional losses in the screw-threads account for most of the mechanical damping in the system, so that well-fitting threads are called for." (p. 301) - Maropis — Jones patent. Square threads. zzz
Flatness and parallelism
All mating surfaces should have high flatness. Preferably the required flatness can be substantially achieved during the machining process. However, final lapping (either by hand or machine) is recommended. Prokic (1) (p. 6-5) recommends 600 grit (or higher) polishing paper on a lapping machine that produces only planar (X-Y) motion. Each ceramic should be lightly pressed on each side for 5-10 seconds. The front driver and back driver can be laped under their own weights. (Note — hand lapping requires extreme care so that the surface doesn't become convex due to uneven lapping pressure.)
The faces of the ceramics must be parallel to high tolerances.
If sufficient flatness or parallelism cannot be otherwise achieved then some investigators have recommended placing a conductive metal film at each interface. (See Branson patent 3,066,232, p. 3.) This film should be relatively soft (so as to flow into any voids) and nonozidizing. Soft nickel has been suggested (Branson patent 3,066,232, p. 3).
Silver-filled epoxy resins have also been suggested. (See Jones (1), p. 15.) However, achieving a consistently uniform resin thickness may be difficult. This also complicates the assembly process.
Assembly
All components should be ultrasonically cleaned just prior to assembly.
An alignment fixture should be used during assembly to assure that all of the parts are centered with respect to the front driver. This can be done with a machined plastic sleeve that has cutouts for the electrodes. The sleeve's inside diameter is just slightly larger than the ceramic stack. After the sleeve has been slid over the back driver and ceramic stack, it is positioned about a reference surface (e.g., the front driver's mounting flange) and the stack bolt is tightened. The sleeve is then removed.
Transducer failure modes
The following are common failure modes for transducers.
Ceramic overheating
As the ceramic temperature increases the ceramic electromechanical properties change, generally in a nonlinear manner. This changes the transducer's performance. For example, see figure 28. If the temperature is not too high then the change may be reversible; otherwise, the change will be permanent.
|
|
|
DeAngelis - local high prestress (nonuniform prestress) zzz
Although the maximum temperature is often simply specified as a percent of the Curie temperature (e.g., 50% - Waanders, p.6), this is a very inexact guideline. For example, "The material's temperature limitation decreases with greater continuous operation or exposure." (Vernitron, p. 14) Another reference (zzz) indictes that the allowed temperature decreases as the static prestress increases. These concerns fall into two categories —
- The ceramic properties may be permanently altered.
- The performance of the transducer (e.g., the amplitude) may change as the temperature increases, regardless of whether these changes are ultimately reversible when the transducer cools.
Some specific recommendations —
- Branson limits the temperature of PZT8 to 60°C.
- For PZT8 Prokic (1) (p. 4.46) suggests a preferable limit of 60°C but in any case not more than 90°C for continuous (heavy duty) operation. "If piezoceramics in operation reach temperatures between 150°C and 180°, efficiency of transducer will drop significantly." (p. 4.46)
- Bromfield (1) (p. 10) suggests a temperature limit of 60°C.
- For atomization transducers Berger (1) recommends a limit of 150°C (p. 102).
Electrical arcing
|
|
|
Stack bolt failure
Shifted or cracked ceramics
Shifted or cracked ceramics generally result when there is some unbalance in the stack or when the stack is subjected to some type of shock loading (e.g., hammering against a metal insert).
As an example of an unbalance problem, figure 30 shows a Branson metal welding apparatus (per Shoh (2)). The original prototype was 10 kHz with Ø76 mm ceramics. Despite applying huge torque (1m wrench + 1m extension + 2 men) to the stack bolt, the ceramics repeatedly failed by slipping and cracking. This was caused by unbalance in the horn due to the welding tip (part 40) which was offset from the stack centerline, thereby causing flexure waves in the stack. The problem was initially solved by inserting a plug on the opposite (top) side of the horn in order to counterbalance the weight of the offset welding tip. (Culp)
|
||||||||||
|
The problem of unbalance also occurs in contoured horns and medical probes that are bent. The unbalance in contoured horns can be reduced by shifting the contour location or by reducing the contour depth. The unbalance in bent medical probes can be improved by changing the size or location of the bend radius.
|
|
|
The problem of shifted ceramics can be reduced if appropriate platings are used on the ceramics and electrodes. After assembly (and possibly some run-in time) the ceramics and electrodes become a zzz monolythic stack by diffusion bonding. (See above.) Then, individual ceramics can't shift; instead, the entire stack must shift.
|
|
|
Fatigued electrode tabs or wires
Testing prototype designs
Loss tests
Transducer losses have two components — electrical losses and mechanical losses. It is desirable to distinguish between these so that they can be separately minimized.
Electrical losses
Electrical losses are primarily dielectric although some ceramic resistance is also present. With a well-designed and well-assembled transducer, these are the losses that cause ceramic heating.
Electrical losses can be determined by two methods.
- With a single transducer, each pair of ceramics is driven such that the voltages are 180° out of phase (i.e., when the voltage on one ceramic is positive, the voltage on the adjacent ceramic is negative, and vice versa). Krueger (1) (Appendix A, p. 8) used this method.
- Two nominally identical transducers are assembled as shown in figure 35. In this case, both transducers are simultaneously driven in-phase by the same power supply (rather than having the test transducer connected to a load).
In both methods the drive frequency is the normal operating frequency.
In the first method each pair of ceramics is attempting to expand or contract at the same time. In the second method both transducers are attempting to expand or contract at the same time. In both methods the resulting opposition forces prevent the transducers from vibrating. Thus, all mechanical (vibrational) losses are removed, leaving only the electrical losses. (In the second method the electrical losses from both transducers.)
Note — The second method is more physically complicated and may also require power supply adjustments in order to compensate for the capacitance of two transducers (rather than a single transducer).
This test would be useful when evaluating ceramics from different manufacturers, assuming that the ceramics are otherwise prepared to the same mechanical specifications (flatness, parallelism, finish, etc.). This can also help to determine if there is a drive level at which the losses suddenly start to increase. Then the drive level should be kept below this critical limit except for short burst intervals.
Mechanical losses
Mechanical losses result from straining of the various components and from friction at the interfaces (at the ceramic faces, the bolt threads, etc. These losses can be determined by operating the transducer under power (see the power loading tests) and then subtracting the electrical losses as determined above.
The measured mechanical losses can be used to see the effect of changing surface finishes, ceramic insulation materials, thread locations and specifications, etc.
Power (loading) tests
To a large extent the power a transducer can deliver depends on the ability to maintain an acceptable ceramic temperature. For a given design this means that ceramic heat must be removed, both by conduction and convection. As the delivered power increases the power dissipated in the ceramics also increases. Thus, conduction may be effective at low power but convection is necessary at higher power. At even higher power convection may not be sufficient in which case the duty cycle must be reduced (i.e., the transducer's nominal power must be derated).
The transducer must be loaded in steps in order to determine its power handling capability. The loading procedure is —
- Machine a longitudinal slot in the housing through which the ceramics are visible. Cover this slot with a transparent plastic film to prevent cooling air from escaping. This slot will be used to measure the ceramic temperature with an infrared thermometer.
- Specify —
- The maximum acceptable ceramic temperature. (affected by prestress - See zzz.)
- The "on time" for when the duty cycle is less than 100%. The on-time will depend on the intended application. For example, for ultrasonic plastic welding the on-time might be specified as 2 seconds. For an ultrasonic medical device the on-time could be significantly longer. (zzz average or max?)
- Set the air flow rate for the subsequent series of tests.
- Start with a 100% duty cycle (i.e., continuous ultrasonics).
- Adjust the load to achieve a specified input power (typically as measured with a wattmeter).
- Maintain the ultrasonics until the temperature of the ceramics has stabilized. The temperature should be measured at the ceramic with the highest temperature (typically the ceramic closest to the node).
- If the stabalized temperature is less than the maximum acceptable temperature then record the data and increase the load (i.e., increased power). Repeat steps 5 and 6.
- If the stabalized temperature exceeds the maximum acceptable temperature then reduce the duty cycle (i.e., increase the "off time" while maintaining a consistent "on time"). Repeat steps 5 and 6.
- Repeat steps 5 and 6 at increasing loads until either the maximum expected power has been achieved or the lowest expected duty cycle has been achieved.
zzz Monitor amplitude?
The above procedure should be repeated for several well-aged transducers so that an average can be determined. The following graph shows the results of loading tests for a single 15 kHz transducer whose design is similar to that of figure 1.
|
|
|
|
(Note: SCFM = Standard Cubic Feet per Minute.)
Thus, given sufficient air flow, the transducer can operate at 100% duty cycle (i.e., continuous sonics) up to about 1700 W. For any power above 1700 W, the duty cycle must be decreased in order to maintain the ceramic temperature. At 3500 W the duty cycle must be reduced to 50% for 80 SCFM and 35% for 50 SCFM — i.e., the transducer must be derated from its operation at continuous sonics. Hence, three parameters must be specified when listing a transducer's power rating — 1) the power output, 2) the cooling fluid (typically air) and the flow rate, and 3) the duty cycle.
For this 15 kHz transducer the total ceramic volume was 98 cm3. Then the graph of figure 33 can be normalized to give the power densigy (watts per unit volume of ceramic volume).
|
|
|
|
Then, given sufficient air flow, the transducer can operate with continuous sonics up to about 17 W/cm3 of ceramic or 35 W/cm3 of ceramic at 50% duty cycle and 80 SCFM. Dividing by the frequency in kHz gives 1.2 (W/cm3)/kHz and 2.3 (W/cm3)/kHz, respectively. These values are consistent with those of table 7 for a transducer with offset ceramics.
Loading methods
In order to determine the transducer's power handling capability, it must be loaded so as to maintain a reasonably stable power level until the ceramic temperature has stabilized. Two methods are commonly used.
Water loading
For water loading the transducer is connected to a booster and horn (typically a bell horn). The horn is then immersed in water until the desired power has been achieved. The horn should be immersed at least 15 mm to avoid power fluctuations due to surging water around the horn's face. The booster may need to be changed in order to achieve the desired operating conditions. During the test the power may vary somewhat as the transducer's amplitude drifts. (This drift would be due to ceramic heating and frequency drift, and would depend on the ability of the power supply to compensate.) However, the power can easily be adjusted by changing the horn's immersion depth.
Electrical loading
For electrical loading the test transducer is driven by a drive transducer which is connected to a power supply. An intermediate booster may be used to provide gross amplitude adjustment to the test transducer. In some cases the intermediate booster may be required in order to stabalize the system, even if the booster has just 1:1 gain. The terminals of the test transducer are connected to a variable electrical load (e.g., a high-power resistor) or electronic load. A wattmeter measures the output power to the load. (This power measurement does not include any power that is dissipated within the test transducer. Hence, if this transducer were used in an actual application, rather than in this test situation, then this measured power would represent the input power to the transducer (i.e., as measured by a wattmeter).) Figure 35 shows the arrangement (after Hampton (1), p. 58).
|
|
|
For this arrangement the driving and test transducers should have the same nominal frequency. However, the design of the test transducer could be completely different than the driving transducer. Thus, a new transducer design could be driven by an off-the-shelf transducer and power supply. Then the power characteristics of the test transducer could be evaluated independently and in parallel with the development of its new power supply.
Arcing tests
Sensitivity to unbalanced horns
Performance
Amplitude
Typical 20 kHz half-wave transducers have output amplitudes in the range of 10 to 20 microns (peak‑to‑peak) at no‑load. With properly designed power supplies, this no‑load amplitude can be substantially maintained under load.
The amplitude can be increased by increasing the drive voltage. However, there is a limit to the allowed voltage depending on the resulting field strength (volts/mm of ceramic thickness) which, in turn, depends of the chosen ceramic thickness. As the voltage increases, the chance of electrical arcing increases.
When a transducer is operated at parallel resonance the amplitude is proportional to the ceramic capacitance. The amplitude can be artifically increased by adding an external capacitor in parallel with the ceramics. However, this will decrease the parallel resonant frequency somewhat and the loss will increase because of the current flow through the external capacitor. Also, the power supply may need to be adjusted to accommodate the increased capacitance. (Since series resonance is essentially unaffected by ceramic capacitance, adding the external capacitor will have little effect.)
Power
The maximum available power at a given frequency depends on the transducer's ability to store energy and a requirement to limit the temperature of the ceramics. The stored energy is composed of the mechanical strain energy and the electrical capacitive energy.
- Mechanical strain energy. Mechanical strain energy will be high when the ceramics are highly dynamically strained. However, this may lead to fatiguing of the ceramics and the attached mechanical components, particularly the stack bolt and front driver (if aluminum). Ceramic fatiguing can be reduced by using a high static prestress but this may lead to reduced output due to reduced \( d_{33} \) and increased loss due to increased \( tan \delta \). Thus, there is a limit to the strain in a transducer.
- Electrical capacitive energy. Electrical capacitive energy will be high when there is a high effective volume of ceramic. (Note that a ceramic is most effective when it is located near the transducer's nodal region.) A high electric field strength is also helpful but can lead to arcing and increased loss due to increased \( tan \delta \).
Note that the factors that determine energy storage are interdependent. Thus, the estimation of maximum power is very complicated and is generally best determined experimentally.
The final consideration is the maximum allowed ceramic temperature. This maximum temperature is often expressed as a percent of the Curie temperature \( T_c \). Thus, if the Curie temperature could be increased then, in theory, the transducer could develop more power without overheating. Unfortunately, modifying the ceramic composition to increase the Curie temperature generally results in reduced \( d_{33} \). (Figure 36 shows this trend for various ceramics from Piezo Technologies (2), p. 2. Note, for instance, that the bismuth titanate compositions (diamond symbols) have very high \( T_c \) but very low \( d_{33} \). Also note that the vertical scale is logarithmic.)
Reduced \( d_{33} \) may be tolerated if a lower output amplitude from the transducer is acceptable (e.g., if gain can be increased elsewhere in the ultrasonic stack). If not then the transducer must be designed with more "gain" or, alternately, the transducer must be driven harder to achieve the same output amplitude. The former approach may not be possible due to dimensional limitations; the latter will result in increased \( tan \delta \) which will therefore increase the temperature further. (Note that modifying the ceramic composition to increase the Curie temperature may have other side effects so the ceramic manufacturer should be consulted.)
|
|
|
Assuming that the transducer's safe strain is not exceeded (i.e., no mechanical failure of the ceramics) then the available power depends on the ability to maintain acceptable ceramic temperature. Since the ceramic temperature depends on the duty cycle and the amount of forced cooling (cubic liters/sec), these values must be specified in order to properly evaluate reported power output. The following table estimates the maximum power available, based on the total volume of ceramic. (Note: some references have reported the maximum power in relation to the ceramic cross-sectional area. This method is not correct since the maximum power depends on the total volume of ceramic.)
|
|||||||||||||||
|
The following are assumed for the reported estimates but could not be verified in some cases.
- Ultrasonics are applied reasonably continuously.
- Ceramics are adequately cooled.
- No distinction is made between series and parallel resonance, although such distinction may exist.
Jones (p. 14) states, "... PZT-4's theoretical maximum under reasonably high loading (Q —> 1) being as aforesaid 6 watts per cubic centimeter per kilocycle ..." However, Jones gives no specific reference for this value.
Note that the power density (W/cm3) increases with the frequency. ("When a given design is scaled in frequency, its watts/lb figure will be directly proportional to frequency." Woollett (2), p. 92)) For example, using Wuchinich's estimate for a transducer with offset ceramics, the power density at 20 kHz is 1.5 W/cm3*20 kHz = 30 W/cm3 whereas this increases to 60 W/cm3 at 40 kHz. However, if the dimensions of a 20 kHz transducer are scaled exactly by 1/2 to produce a 40 kHz transducer then the ceramic volume is reduced by a factor of 8. Then the total power (W) available at 40 kHz is 1/4 of that at 20 kHz.
Also see Power tests.
Overcoming power limitations
Power delivery is limited by the available volume of ceramic and the ability to adequately cool the ceramics.
Ceramic volume
For a half-wave transducer the total ceramic volume is limited by two considerations.
- Ceramic that is located near the antinodes is relatively ineffective. Therefore, the total length of ceramic is limited to about 1/4 wavelength when the ceramics are centered at the node or 1/8 wavelength when the ceramics are offset from the node. (See the section on optimum ceramic length/placement.)
- Because of the need to apply reasonably uniform prestress across the ceramics, the ceramic diameter is limited to about 1/4 wavelength for a center bolt design. Because of potential problems with Poisson-induced stresses, the actual maximum diameter may be even lower.
In the above, the wavelength is that of the ceramic. This is approximately 160 mm (short circuit) and 210 mm (open circuit) for PZT8 at 20 kHz.
However, the ceramic volume can be increased by the following methods. The transducer then becomes larger (either in length or diameter) so these methods may not be practical (e.g., for small hand-held medical devices). Also, each additional section or component increases the liklihood of conflicting secondary resonances.
Full-wave transducer
A full-wave transducer acts like two half-wave transducers in series. Thus, the ceramic volume is effectively doubled. Of course, because the ceramic groups are separated by a half wave, each ceramic group must be driven out of phase with respect to the other group (i.e., when one group is driven with a positive voltage the other must be driven with a negative voltage).
|
|
|
This design is used by Kulicke & Soffa (figure 38) with four ceramics in each half-wave section. The stack bolt extends through both groups of ceramics and is threaded into the horn which is, by itself, a half-wave section.
|
|
|
Multiple axial transducers
Multiple axial or near-axial transducers can be used to drive a single ultrasonic stack. Compared to a single large diameter transducer, each of the smaller transducers has smaller diameter ceramics which potentially allows a more uniform ceramic prestress.
Because the ceramics have smaller diameter, ceramic heat can be conducted more easily to the ceramic periphery so the ceramics should remain cooler for a given air flow. However, this advantage may be offset if the resulting exposed ceramic peripheral area for convective cooling is smaller than that of the single larger diameter transducer. A heat transfer analysis would be required in order to determine the most effective design.
|
|
|
Multiple stacks
Multiple discrete stacks may be used to increase the total ceramic volume. Proper placement of such stacks may improve the horn's amplitude uniformity and may improve the frequency separation. However, the opposite effects may also occur.
In addition, circulating currents among the transducers may cause problems. See Branson patent zzz (Allan Roberts).
|
|
|
Multiple radial transducers
Multiple transducers (typically four or six) can be arrayed radially around a central hub. This hub then uses Poisson coupling to transform the radial motion into axial motion along the axis of the hub. Although the potential power delivery is very large, this arrangement is quite bulky and is generally best suited to processing-type applications. The following figure shows a design by Watanabe (1) that uses a radially resonant disk with 12 driving transducers.
|
||||||||||
|
Cooling
Cooling may be required to keep the ceramics from exceeding a safe operating temperature (usually specified as some percent of the Curie temperature). The safe temperature will depend on the ceramic type as well as operating parameters; for example, the ceramic prestress decreases the safe operating temperature. zzz
Air cooling
Forced air is the most common method of cooling. The air is generally introduced at the back of the housing and then passes over the outside of the back driver and the ceramics. The air then exits through a series of peripheral holes in the front driver (figure 2), thereby cooling the front driver and extracting further heat from the ceramics. In this case an aluminum front driver can help to conduct heat away from the ceramics.
Note — Before entering the transducer the cooling air should first pass through a filter to remove any entrained water vapor. Otherwise, this water vapor will be deposited on the exposed ceramic surfaces and may cause arc-over between the electrodes.
If the transducer must be splash proof then the exhaust air can be extracted through an exit tube, typically at the rear of the housing.
|
|
|
Cooling disks (heat sinks) between the ceramics and which extend beyond the ceramic peripheries have been suggested to provide additional conductive/convective heat transfer. The disks may also have radial channels through which air can flow. (See the section on electrodes.) Such disks are most effective if they have high thermal conductivity (e.g., aluminum).
Figure 43 shows a half-wave design (Roberts patent 6,434,244‑B1, 2002) that uses a central cylinder (11) and a back driver (5) with radial cooling fins. In addition, this design uses ceramics (7 and 9) that are symmetrically located about the transducer's node. (This centered ceramic arrangement, which maximizes the electromechanical coupling, is well known to be superior to an offset ceramic location. Roberts cites the offset ceramic arrangement as the prior art for comparison purposes.) This design gives lower and more uniform ceramic temperature, both axially and radially. This patent indicates that a finned transducer with symmetric ceramics can handle as much as 33% greater higher power than otherwise (p. 7), although it doesn't distinguish the separate contribution of each design technique. zzz More unform ceramic prestress due to longer back driver.
|
|
|
Figure 44 shows an earlier patent by Williams 3,689,783 (1972). This design also uses a radially finned cylinder (39) for improved conductive/convective heat transfer. Although this is a full-wave design, the concept is obviously similar to Roberts' design (which doesn't cite Williams' patent as prior art) so this may question the legitimacy of Roberts' patent. (Also see the Scarpa patent 3,140,859 (1964) shown in figure 27.)
|
|
|
In some cases cooling air can flow to the interior bore of the ceramics (see figure 4). However, implementation may not be convenient for a center bolt design. Also, the interior bore of the ceramics is generally not coated with an insulating film so any moisture in the cooling air will coat the bore and may increase the possibility of electrical arcing between ceramics. (In general, the cooling air should be dehumidified to reduce arcing.)
Liquid cooling
Liquid cooling may be more effective than air cooling. (In fact, liquid cooling is generally needed for magnetostrictive transducers since the laminations are relatively lossy.) However, the liquid will absorb energy, principally through the back driver, so the transducer efficiency is reduced. Jones (patent 3,283,182, p. 7) tried using transformer oil; this improved the cooling compared to forced air but reduced the overall efficiency due to coupling of vibration through the oil to other portions of the assembly. However, liquid cooling may still be reasonable if coupling from the back driver could be reduced, for example by attaching a non-coupling material (possibly rubber or something similar). Of course, liquid cooling requires a water-tight housing. Pumps and other equipment may also be needed.
Johnson's patent 2007/0080609 A1 includes the use of a thermally conductive gel in the interior space between the stack bolt and the ceramics. The specifics of the gel and the method of introduction are not discussed. Presumably the gel could be introduced through an external orifice (e.g., in the back driver) which would then be sealed.