Bessel function

A function that is the solution to the differential equation —

\begin{align} \label{eq:11101a} x^2 \, \frac{d^2y}{dx^2} + x \, \frac{dy}{dx} + (x^2 - p^2) \, y = 0 \end{align}

where —

p	= a complex number (the order of the Bessel function)

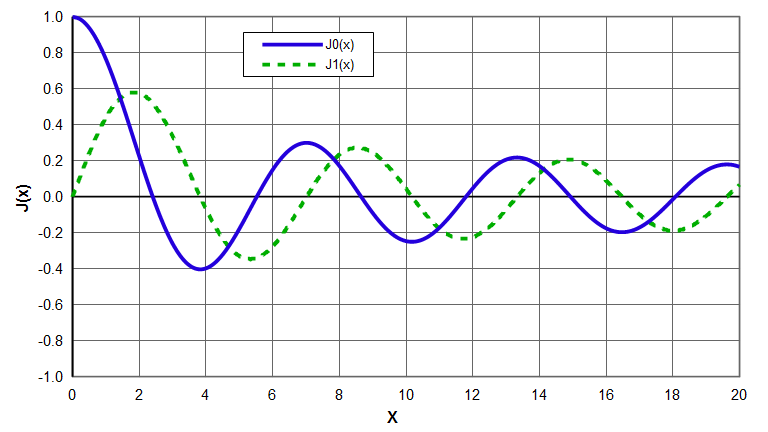
Two common Bessel functions are shown in the following graph. Note that \( J_0(x) \) resembles a decaying cosine while \( J_1(x) \) resembles a decaying sine.

Figure 1. Bessel functions - J0(x) & J1(x)

Modified Bessel function

A function that is the solution to the differential equation —

\begin{align} \label{eq:11102a} x^2 \, \frac{d^2y}{dx^2} + x \, \frac{dy}{dx} - (x^2 + p^2) \, y = 0 \end{align}

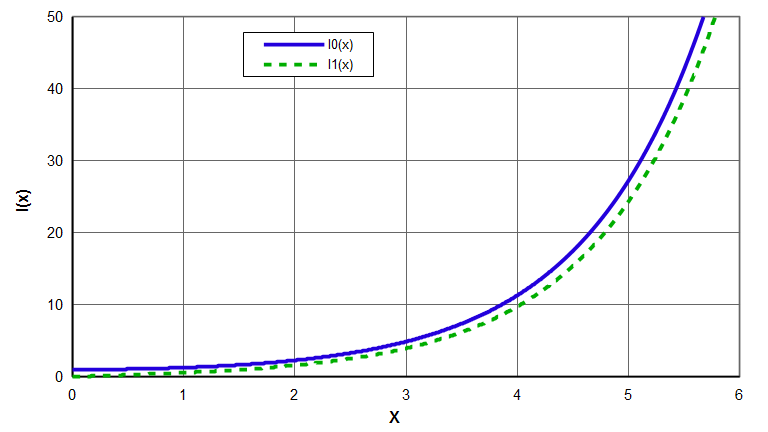
Two common modified Bessel functions are shown in the following graph. Note that \( I_0(x) \) resembles a hyperbolic cosine while \( I_1(x) \) resembles a hyperbolic sine.

Figure 2. Modified Bessel functions - I0(x) & I1(x)

Bessel functions and modified Bessel functions describe the flexural and radial vibration of disks and the axial amplitude of a pressure wave in an infinitely long cylinder (and many other physical phenomena).

References:
Abramowitz, pp. 355 - 434.
Kinsler, pp. 449 - 452 — includes tables for Bessel functions \( J_0(x) \), \( J_1(x) \), and \( J_2(x) \) and modified Bessel functions \( I_0(x) \), \( I_1(x) \), and \( I_2(x) \)
Wikipedia