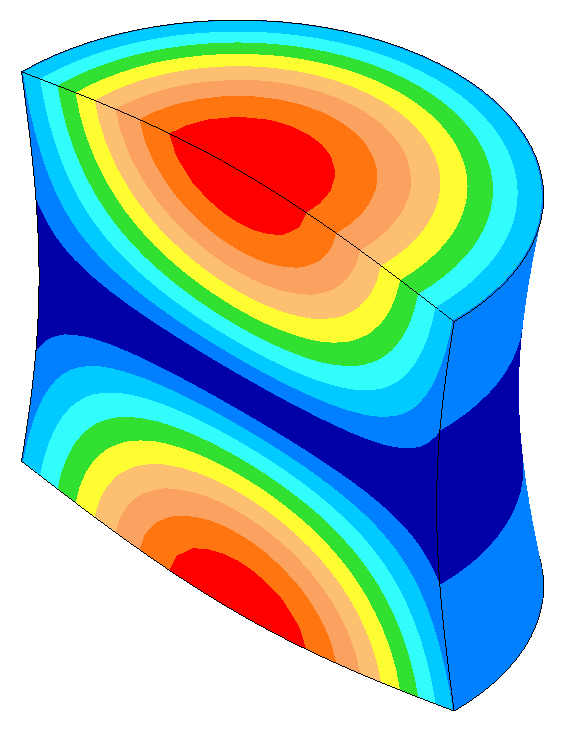
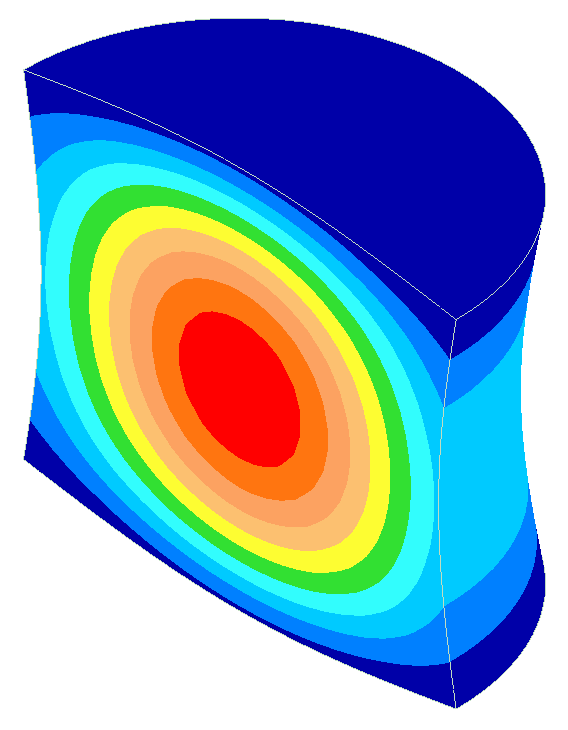
Prismatic resonator
Contents
- Axial amplitude
- Axial strain and stress
- Tuning
- Relative amplitudes
- Effect of Poisson's ratio
- Appendix A. Tuned length of a cylindrical prismatic resonator (Rayleigh and Mori approximations)
- Appendix B. Tuning rate of a thin prismatic resonator
- Appendix C. Energy stored in a thin longitudinally resonant member
This page discusses the performance prismatic resonators (i.e., where the cross-sectional dimensions are constant in the principal direction of vibration).
Unless otherwise indicated —
- The resonators are cylindrical.
- The resonators do not contain a stud or stud hole.
- The primary vibration mode is axial. (For very large diameter resonators the radial amplitude may exceed the axial amplitude. None-the-less, the axial mode is the mode of investigation.)
- Amplitudes, strains, and stresses are determined along the resonator's axis centerline.
- Performance data have been determined by finite element analysis (FEA).
Axial amplitude
The axial amplitude of a prismatic resonator is cosinusoidally distributed along the resonator's length from the free end —
\begin{align} \label{eq:10701a} u(x) &= U_p \cos \left( \frac{\pi}{\Gamma} \, x \right) \end{align}
where —
| \( u \) | = amplitude distribution |
| \( x \) | = distance, starting from a free end (antinode) |
| \( U_p \) | = maximum (peak) amplitude |
| \( \Gamma \) | = half wavelength at the resonant frequency |
The quantity in ( ) is in radians. The amplitude \( u(x) \) is maximum at the antinodes (the free end and every half wavelength (\( \Gamma \)) thereafter). \( u(x) \) is zero at the nodes (\( \Gamma/2 \) and every \( \Gamma \) thereafter). For a thin wire \( \Gamma \) is simply the thin-wire half wavelength \( \Gamma_{tw} \).
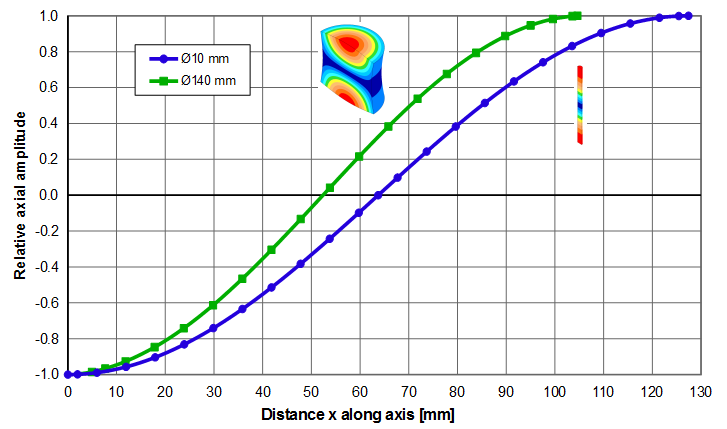
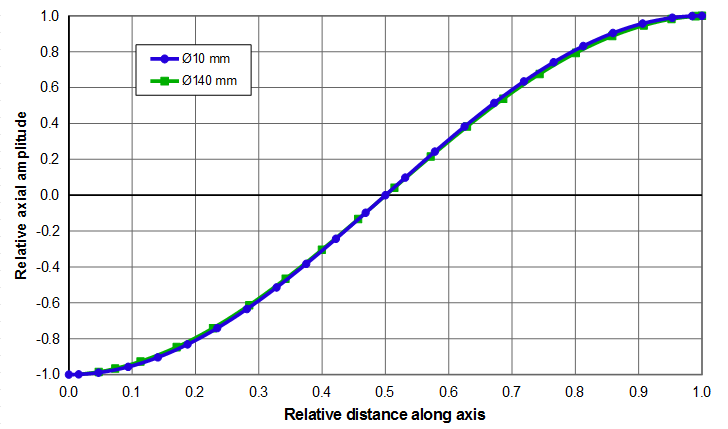
Equation \eqref{eq:10701a} applies regardless of whether the resonator is thin or fat. This is illustrated for the two 20 kHz resonators of figure 1 — a \( \phi \)10 mm which is reasonaby thin and a \( \phi \)140 mm which is decidedly fat. The amplitude data along each resonator's axis are graphed in figure 2. The data in the left panel show the amplitude distributions that correspond to the actual resonator lengths. The right panel shows the same data but where the X-axis has been normalized with respect to the half wavelengths of the two resonators — i.e., \( \large\frac{x}{\Gamma_{\phi 10}} \) and \( \large\frac{x}{\Gamma_{\phi 140}} \). The two curves in the right panel are nearly coincident showing that both the thin and fat resonators can be described by equation \eqref{eq:10701a}.
|
||||||||||
|
|
||||||||||
|
Axial strain and stress
A thin wire experiences strain only in the axial direction. Then the axial strain is the derivative (slope) of the amplitude curve —
\begin{align} \label{eq:10702a} {\epsilon}(x) &= \frac{du}{dx} \\[0.7em]%eqn_interline_spacing &= U_p \left( {\frac{\pi}{\Gamma_{tw}}} \right) \sin \left( {\frac{\pi}{\Gamma_{tw}}} \, x \right) \nonumber \end{align}
The strain \( {\epsilon}(x) \) is zero at the antinodes (the free end and every half wavelength (\( \Gamma_{tw} \)) thereafter). \( {\epsilon}(x) \) is maximum at the nodes (\( \Gamma_{tw}/2 \) and every \( \Gamma_{tw} \) thereafter).
\begin{align} \label{eq:10707a} {\epsilon}_{max} &= U_p \left( {\frac{\pi}{\Gamma_{tw}}} \right) \end{align}
Rather than expressing the above equations in terms of the half wavelength, they may be more conveniently expressed in terms of the frequency and wave speed where it is recognized that —
\begin{align} \label{eq:10703a} \Gamma_{tw} = \frac{c_{tw}}{2 \, f} \end{align}
where —
| \( c_{tw} \) | = Thin-wire wave speed = \( \sqrt{\frac{E}{\rho}} \) |
| \( f \) | = frequency |
Then equations \eqref{eq:10701a} through \eqref{eq:10707a} become —
\begin{align} \label{eq:10704a} u(x) &= U_p \cos \left( {\frac{2\pi \, f}{c_{tw}}} \, x \right) \end{align}
\begin{align} \label{eq:10705a} {\epsilon}(x) &= U_p \left( {\frac{2\pi \, f}{c_{tw}}} \right) \sin \left( {\frac{2\pi \, f}{c_{tw}}} \, x \right) \end{align}
\begin{align} \label{eq:10706a} {\epsilon}_{max} &= U_p \left( {\frac{2\pi \, f}{c_{tw}}} \right) \end{align}
Fat resonators
As discussed above, the amplitude along the resonator axis is cosinusoidal (equation \eqref{eq:10701a}), regardless of whether the resonator is thin or fat. However, the strain equation \eqref{eq:10702a} only applies when the strain acts in a single direction, which is true for thin resonators. Fat resonators will have higher net strain due to two effects —
- In addition to the axial motion, fat resonators also have lateral "breathing" motion due to Poisson coupling. This results in additional radial and circumferential (hoop) strains.
- Fat resonators have a shorter tuned length (i.e., \( \Gamma \lt \Gamma_{tw} \)) so a given amplitude will be contrained within a shorter length.
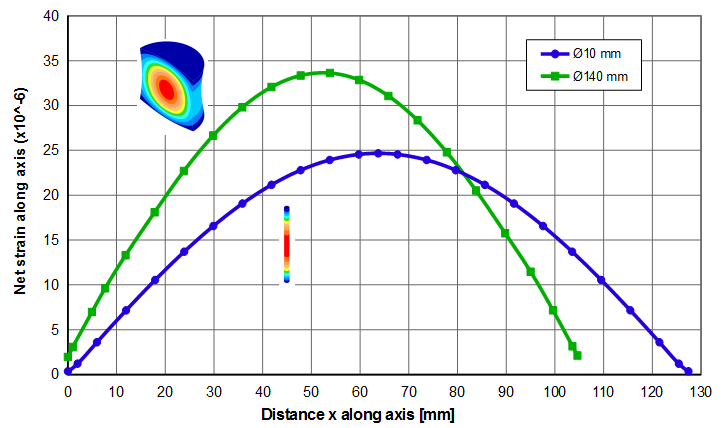
The net result of these two effects is shown in figures 3 and 4 for a 20 kHz resonator. The \( \phi \)10 mm resonator is reasonably thin and its strain can be predicted from equation \eqref{eq:10702a}. On the other hand the \( \phi \)140 mm resonator is substantially fat —
- Its half wavelength is 18% shorter than the thin resonator (105 mm versus 127 mm).
- Its peak strain is 36% higher than the thin resonator.
- The strains at the free end faces (antinodes) are not zero; instead, they are 6% of the strain at the node. This is because the free ends have substantial radial amplitude (5% of the face axial centerline amplitude).
|
||||||||||
|
|
|
|
Note: The net strains shown above are the von Mises strains. The von Mises stress can then be calculated as the product of Young's modulus \( E \) and the von Mises strain.
Tuning
The tuning of a prismatic resonator depends on the ratio of the resonator's diameter to its prismatic half wavelength.
Tuned length
The tuned length of a thin prismatic resonator is —
\begin{align} \label{eq:10710a} \Gamma_{tw} = \frac{c_{tw}}{2 \, f} \end{align}
where —
| \( \Gamma_{tw} \) | = thin-wire half-wavelength |
| \( c_{tw} \) | = thin-wire wave speed |
| \( f \) | = frequency |
The thin-wire wave speed can be determined from the material properties —
\begin{align} \label{eq:10711a} c_{tw} &= \sqrt{\frac{E}{\rho}} \end{align}
where —
| \( E \) | = modulus of elasticity (Young's modulus) |
| \( \rho \) | = density |
As the lateral dimensions of the resonator increase (i.e., the resonator is no longer "thin"), the half-wavelength decreases below that of a thin wire. From a physical standpoint, when the resonator's diameter is larger than an infinitely thin wire then radial "breathing" occurs due to Poisson's coupling. This radial motion imparts additional kinetic energy which would cause the resonator's frequency to drop. In order to maintain the desired frequency the resonator's length must be reduced.
At larger diameters even more breathing occurs and the resonator must tune progressively shorter. At the largest possible diameter the resonator is reduced to a thin flat disk. Then the breathing is simply the fundamental radial resonance of the disk.
The actual tuned length at a finite diameter \( D \) can be determined by multiplying \( \Gamma_{tw} \) by a length factor \( K_L \).
\begin{align} \label{eq:10712a} \Gamma = K_L \,\, \Gamma_{tw} \end{align}
where —
| \( \Gamma \) | = half-wavelength at diameter \( D \) |
| \( \Gamma_{tw} \) | = thin-wire half wavelength |
| \( K_L \) | = tuned length factor |
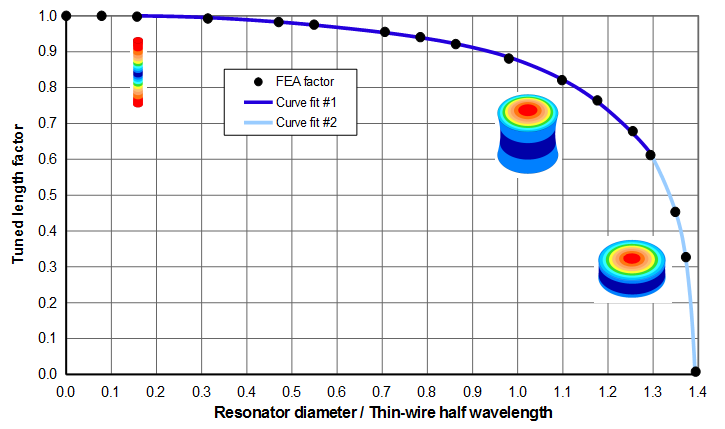
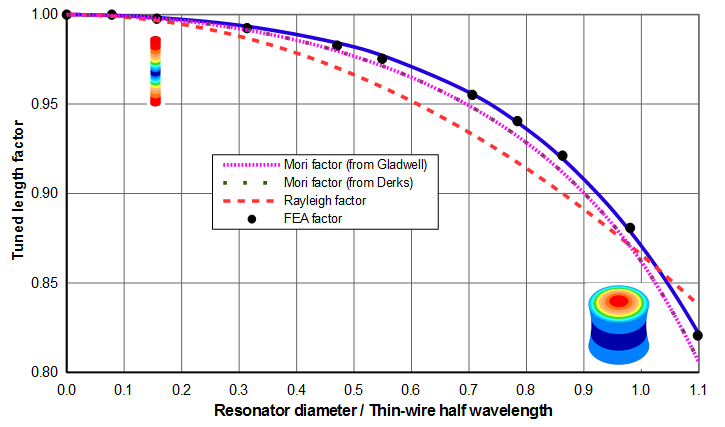
The tuned length factor can be determined from figures 5 or 6 or the associated curve fit equations. Note that figure 6 is simply a zoomed portion of figure 5 where the horizontal axis is limited to 1.1. This is typically the largest value for cylinders that are longitudinally resonant. The images in the figures show the relative sizes of the cylinders and their axial amplitudes (parallel to the cylinder's axis.)
(Note: Two theoretical approximate length factors — the Rayleigh factor \( K_{L_R} \) and the Mori factor \( K_{L_M} \) — are discussed in Appendix A.)
|
|
|
|
|
|
Curve fits
In order to fit the data reasonably well, two polynomial curve fits are used for the data of figures 5 and 6 —
For \( X \le 1.3 \) (dark blue curve) —
\begin{align} \label{eq:10713a} K_L = 1 - 0.0255 \, X^2 - 0.2861 \, X^3 + 0.4793 \, X^4 - 0.2932 \, X^5 \end{align}
For \( X \ge 1.3 \) (light blue curve) —
\begin{align} \label{eq:10713b} K_L = -451.5 + 670.0 \, X - 248.3 \, X^2 \end{align}
where —
| \( X \) | = Cylinder diameter / Thin-wire half wavelength |
| = \( D/\Gamma_{tw} \) | |
| \( K_L \) | = Tuned length factor |
Example 1
Given — a 20 kHz \( \phi \)90 mm cylindrical resonator. The resonator material has a thin-wire wave speed \( c_{tw} \) of 5100 m/sec and a Poisson's ratio of 0.33.
Determine — the tuned half wavelength \( \Gamma \).
- \( \Gamma_{tw} \) = 127.5 mm (equation \eqref{eq:10710a})
- \( D/\Gamma_{tw} \) = 90.0/127.5 = 0.706
- \( K_L \) = 0.954 (from either figure 5 and 6 (which are appropriate for this material) or from equation \eqref{eq:10713a})
- \( \Gamma \) = 0.954 * 127.5 mm = 121.6 mm (from equation \eqref{eq:10712a})
Tuning rate
From Appendix B the tuning rate for a thin prismatic resonator is —
\begin{align} \label{eq:10715a} \varphi_{tw} &= -\frac{f}{n \, \Gamma_{tw}} \end{align}
where —
| \( \varphi_{tw} \) | = thin-wire tuning rate [Hz/mm] |
| \( f \) | = current frequency [Hz] |
| \( \Gamma_{tw} \) | = thin-wire half wavelength [mm] |
| \( n \) | = number of half waves |
Note that the tuning rate is always negative as indicated by the minus sign. However, the tuning rate is generally discussed as a positive (absolute) value.
As the lateral dimensions of the resonator increase (i.e., the resonator is no longer "thin"), the tuning rate decreases (i.e., more material must be removed in order to achieve a given frequency change). This can be accommodated by applying a tuning rate factor to equation \eqref{eq:10715a} —
\begin{align} \label{eq:10716a} \varphi &= K_T \, \varphi_{tw} \\[0.3em]%eqn_interline_spacing &= K_T \, \left( \frac{f}{L} \right) \nonumber \end{align}
Note that equations of this section only apply if the resonator is prismatic. They do not apply if the resonator has gain.
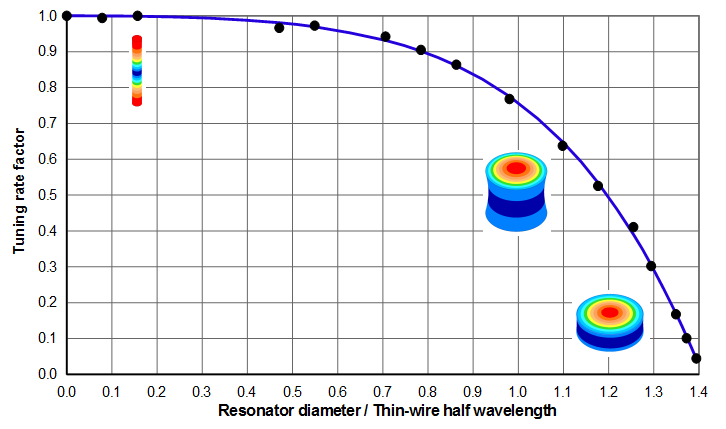
The tuning rate factor can be taken from figures 7 and 8 or the associated curve fit equation.
|
|
|
|
|
|
As discussed above, a resonator tunes shorter as the lateral dimensions increase (i.e., as \( D/\Gamma_{tw} \) increases). It would seem that the tuning rate should then be higher for shorter resonators — i.e., that each unit of length change (in relation to the shortened resonator length) should be more effective in changing the frequency. For example, removing 1 mm from a 127 mm x \( \phi \)20 mm resonator reduces its length by 0.8% whereas removing 1 mm from a 105 mm x \( \phi \)140 mm resonator reduces its length by 1.0%; thus, logic would indicate that the 105 mm resonator should tune more quickly than the 127 mm resonator (assuming both have the same initial frequency).
However, this ignores the effect of the lateral vibration due to Poisson coupling. Thin resonators have relatively little lateral vibration so the kinetic energy is predominately due to longitudinal vibration. As the lateral dimensions increase the resonator's lateral vibration also increases along with a corresponding increase in the lateral kinetic energy. When the resonator is tuned from the face the lateral kinetic energy is relatively unaffected, particularly because this lateral kinetic energy is mainly stored in the nodal region. Thus, more material must be removed from the face of a "fat" resonator in order to change the overall kinetic energy by the same proportion as would be needed to change the kinetic energy of a thin resonator. (This logic that was originally used by Rayleigh for his tuned length correction.) Hence, "fat" resonators tune more slowly than thin resonators. For the above example, the tuning rate for the 127 mm x \( \phi \)20 mm resonator is 157 Hz/mm whereas the tuning rate for the 105 mm x \( \phi \)140 mm resonator is 100 Hz/mm (36% slower).
Curve fit
The polynomial curve fit for the data of figures 7 and 8 is —
\begin{align} \label{eq:10717a} K_T = 1 - 0.0323 \, X^2 - 0.0987 \, X^3 + 0.0262 \, X^4 - 0.1377 \, X^5 \end{align}
where —
| \( K_T \) | = Tuning rate factor |
| \( X \) | = Cylinder diameter / Thin-wire half wavelength |
| = \( D/\Gamma_{tw} \) |
Example 2
Given — a \( \phi \)90 mm x half-wave cylindrical resonator. The length is 124.8 mm for which the frequency is 19500 Hz. The resonator material has a thin-wire wave speed \( c_{tw} \) of 5100 m/sec and a Poisson's ratio of 0.33.
Determine — the tuning rate \( \varphi \) and expected final length.
- \( \Gamma_{tw} \) = 130.8 mm (equation \eqref{eq:10710a})
- \( D/\Gamma_{tw} \) = 90.0 / 130.8 = 0.688
- \( f/\Gamma_{tw} \) = 19500 Hz / 130.8 mm = 149 Hz/mm (thin-wire tuning rate)
- \( K_T \) = 0.94 (from either figure 7 and 8 (which are appropriate for this material) or from equation \eqref{eq:10717a})
- \( \varphi \) = 0.94 * 149 Hz/mm = 140 Hz/mm (from equation \eqref{eq:10716a})
Effect of transducer
Adding a transducer will convert the stack from a half-wave system to a full-wave system and will affect the tuning rate. The exact effect can't be predicted; however, it will depend on the relative stored energy of the resonator compared to the transducer. If the resonator and transducer have similar energy storage then the tuning rate will be close to that of a full-wave prismatic resonator (e.g., \( n = 2 \) in equation \eqref{eq:10716a}). However, if the resonator has relatively high energy storage (e.g., a large diameter steel resonator) then the transducer will have little effect and the tuning rate will be only somewhat less than the half-wave resonator alone (equation \eqref{eq:10716a} with \( n = 1 \) or figures 7 or 8).
Relative amplitudes
As a resonator expands and contracts axially, Poisson coupling causes the resonator to breathe laterally. Such breathing is not uniform but instead predominates where the strain is highest (i.e., at the node). This results in a nonuniform axial amplitude distribution across the resonator's face. See further explanation.
Face axial amplitudes
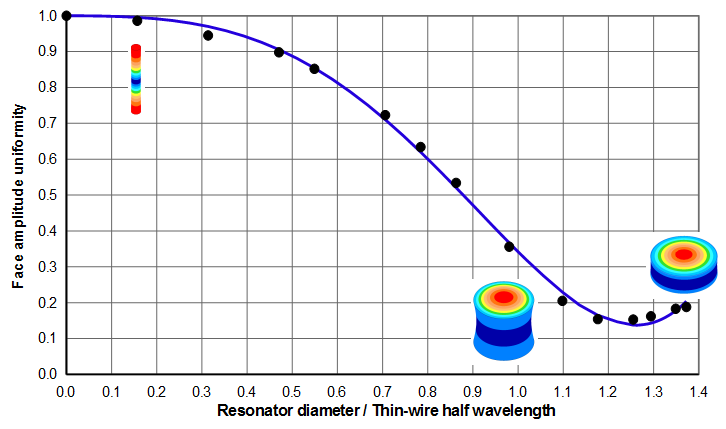
Figures 9 and 10 shows the face amplitude uniformities. (See Uniformity calculation (basic).) Note that figure 10 is simply a zoomed portion of figure 9 where the horizontal axis is limited to 1.1. This is typically the largest value for cylinders that are longitudinally resonant.
|
|
|
|
|
|
Curve fit
The polynomial curve fit for the data of figures 9 and 10 is —
\begin{align} \label{eq:10718a} U = 1 - 0.0809 \, X^2 - 0.5688 \, X^3 - 0.6565 \, X^4 + 0.6481 \, X^5 \end{align}
where —
| \( U \) | = face axial amplitude uniformity |
| \( X \) | = cylinder diameter / thin-wire half wavelength |
| = \( D/\Gamma_{tw} \) |
Radial amplitudes
For the following graphs —
- The radial amplitudes are relative to the the axial amplitude at the center of the resonator's face.
- For reference, the left image of each image pair shows the axial amplitude distribution.
- The arrows show the direction of vibration for the associated colors.
- The colors are chosen so that red represents the maximum amplitude of each imge pair.
- The radial amplitudes are graphed as negative. This simply indicates that the radial amplitudes are out of phase with the axial amplitudes (i.e., when the resonator expands axially the face contracts radially and vice versa).
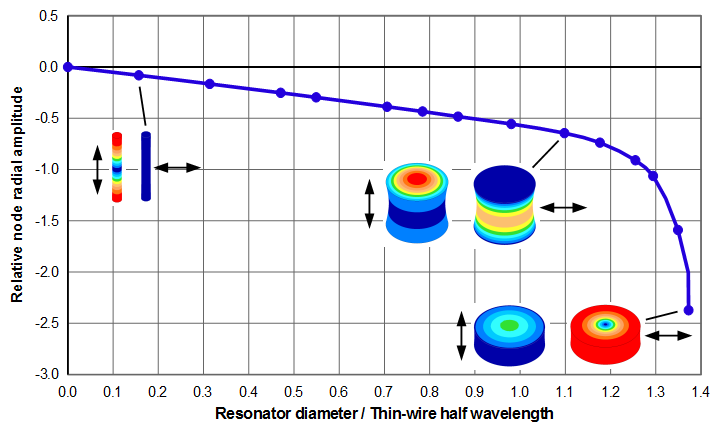
Node radial amplitudes
Figure 11 shows the radial amplitudes at the node.
|
|
|
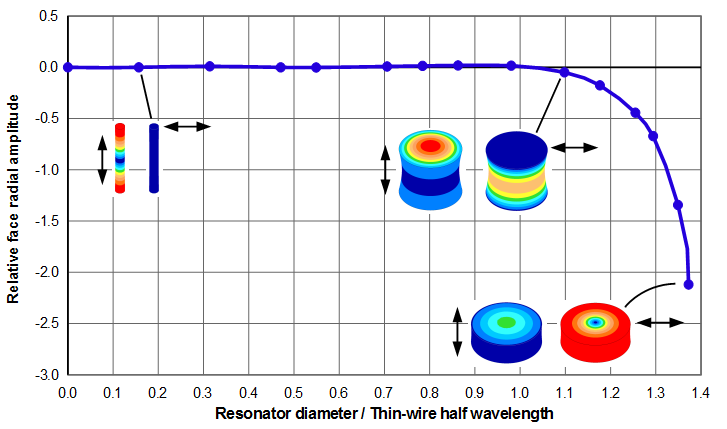
Face radial amplitudes
Figure 12 shows the radial amplitudes at the face periphery. The radial amplitudes are essentially zero until the resonator diameter equals the thin-wire half wavelength (\( \Gamma_{tw} \)); thereafter the radial amplitudes increase rapidly. In fact, as the cylinder becomes more disk shaped the face radial amplitudes approach the node radial amplitudes as can be seen from the coloration of the right-most resonator images.
|
|
|
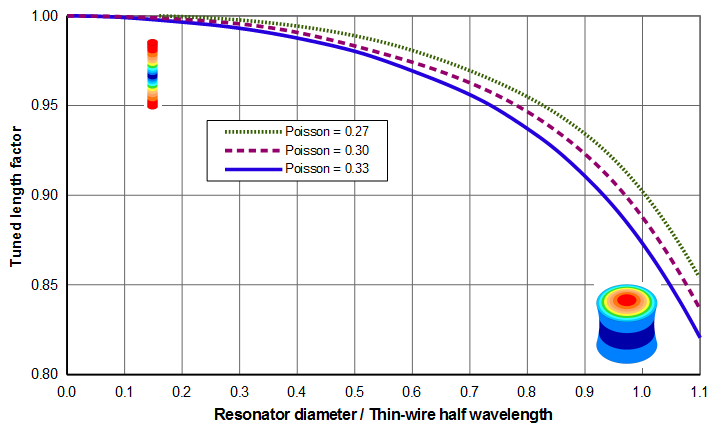
Effect of Poisson's ratio
The above data are for a Poisson's ratio of 0.33. However, the performance will change for different Poisson's ratios. As Poisson's ratio decreases the resonator breathes less. In fact, if Poisson's ratio were zero then resonator would no longer breathe at all and the performance would revert to that of a thin wire, regardless of the resonator diameter. Hence, reducing Poisson's ratio to an intermediate value should have the following effects (assuming that the material's wave speed were unchanged) —
|
||||||||||||||
|
If Poisson's ratio different than 0.33 then, as a first estimate, the performance can be estimated as a linear interpolation/extrapolation —
\begin{align} \label{eq:10719a} Y(\nu) = \left[ \frac{Y(\nu = 0.33) - Y_{tw}}{0.33} \right] + Y_{tw} \end{align}
where —
| \( Y \) | = Performance parameter |
| \( \nu \) | = Poisson's ratio |
| \( Y(\nu = 0.33) \) | = Performance at Poisson's ratio = 0.33 |
| \( Y_{tw} \) | = Performance for thin wire |
Example 3
Given — A 20 kHz \( \phi\)140 mm resonator with a Poisson's ratio is 0.27 (instead of 0.33).
Determine — The performance parameters.
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
Appendix A. Tuned length of a cylindrical prismatic resonator
(Rayleigh and Mori approximations)
For a thin wire the half-wavelength for a pressure wave is —
\begin{align} \label{eq:10750a} \Gamma_{tw} = \frac{c_{tw}}{2 \, f} \end{align}
where —
| \( \Gamma_{tw} \) | = thin-wire half-wavelength |
| \( c_{tw} \) | = thin-wire wave speed |
| \( f \) | = frequency |
The thin-wire wave speed can be determined from the material properties —
\begin{align} \label{eq:10751a} c_{tw} &= \sqrt{\frac{E}{\rho}} \end{align}
where —
| \( E \) | = modulus of elasticity (Young's modulus) |
| \( \rho \) | = density |
As the lateral dimensions of the resonator increase (i.e., the resonator is no longer "thin"), the half-wavelength decreases below that of a thin wire. From a physical standpoint, when the resonator's diameter is larger than an infinitely thin wire then radial "breathing" occurs due to Poisson's coupling. This imparts additional kinetic energy which would cause the resonator's frequency to drop. In order to maintain the desired frequency the resonator's length must be reduced.
At larger diameters even more breathing occurs and the resonator must tune progressively shorter. At the largest possible diameter the resonator is reduced to a thin flat disk. Then the breathing is simply the fundamental radial resonance of the disk.
Rayleigh approximation
Rayleigh (1) (vol. 1, pp. 251 - 252) first developed an equation that approximately accounts for this phenomena for a prismatic cylinder.
\begin{align} \label{eq:10752a} \Gamma = K_{L_R} \,\, \Gamma_{tw} \end{align}
where —
| \( \Gamma \) | = half-wavelength at cylinder diameter \( D \) |
| \( \Gamma_{tw} \) | = thin-wire half wavelength |
| \( K_{L_R} \) | = Rayleigh length factor |
\begin{align} \label{eq:10753a} K_{L_R} = 1 - \small\frac{1}{8} \normalsize \left(\pi \, \nu \, \frac{D}{\Gamma_{tw}} \right)^2 \end{align}
where —
| \( D \) | = resonator diameter |
| \( \nu \) | = Poisson's ratio |
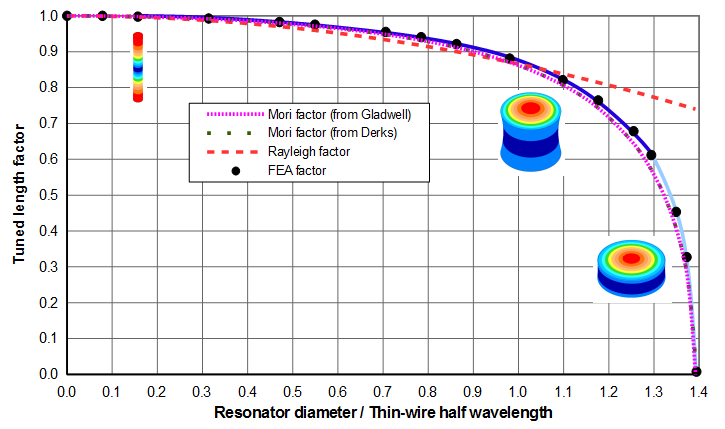
Note that \( K_{L_R} \) depends on the ratio of the resonator's diameter (\( D \)) to the thin-wire half wavelength (\( \Gamma_{tw} \)). When \( D = 0 \), \( K_{L_R} = 1 \) so that \( \Gamma = \Gamma_{tw}\) (i.e., an exact solution). However, as the resonator diameter increases the Rayleigh approximation first under-estimates and then over-estimates the tuned length (figures A1 and A2 for a typical acoustic material).
Mori approximation
Mori (1) improved on Rayleigh's effort by developing an equation that is correct both for a thin wire and, at large diameters, for a radially vibrating disk. The results at intermediate diameters are approximated by a method called "apparent elasticity".
\begin{align} \label{eq:10754a} \Gamma = K_{L_M} \,\, \Gamma_{tw} \end{align}
where —
| \( \Gamma \) | = half-wavelength at cylinder diameter \( D \) |
| \( K_{L_M} \) | = Mori length factor |
\begin{align} \label{eq:10755a} K_{L_M} = \left[ \frac{1 - B_1 \, \psi}{1 - B_2 \, \psi} \right]^{1/2} \end{align}
where —
| \( B_1 \) | = \( 1 - \nu^2 \) |
| \( B_2 \) | = \( 1 - 3 \, \nu^2 - 2 \, \nu^3 \) |
| \( \nu \) | = Poisson's ratio |
| \( \psi \) | \begin{align} \label{eq:10756a} &= \left[ \frac{ \large\frac{\pi}{2} \left(\large\frac{D}{\Gamma_{tw}}\right)}{\alpha} \right]^{2} \nonumber \\[0.7em]%eqn_interline_spacing \end{align} |
| \( D \) | = resonator diameter |
| \( \alpha \) | \( \approx 1.84 + 0.68 \, \nu \) [Derks, p. 42, eqn. 5.8] |
| \( \alpha \) | \( \approx 1.85 \left(1 + 0.386 \, \nu - 0.146 \, \nu^2 + 0.115 \, \nu^3 \right) \) [Gladwell (1), p. 345] |
\( K_{L_M} \) is shown in figures A1 and A2 for a typical acoustic material. Note that the Mori approximation consistently under-estimates the tuned length.
Note that \( \alpha \) is approximate. Derks and Gladwell give somewhat different equations. Derks takes his linear equation from a graph by Kleesattel (2), p. 3, figure 1, curve 1. Kleesattel's graph of this curve is not quite linear so Gladwell's approximation may be somewhat better. However, the difference is small — for \( \nu \) = 0.33 (approximately typical for many acoustic materials), Gladwell's equation gives 2.0666 whereas Dirks' equation gives 2.0639. Figures A1 and A2 shows that the results are nearly indistinguishable.
|
|
|
|
|
|
Appendix B. Tuning rate of a thin prismatic resonator
For a thin prismatic resonator the fundamental wave equation is —
\begin{align} \label{eq:10760a} c_{tw} &= 2 \, \Gamma_{tw} \, f \end{align}
where —
| \( c_{tw} \) | = thin-wire wave speed |
| \( \Gamma_{tw} \) | = thin-wire half wavelength |
| \( f \) | = frequency of longitudinal wave |
Solving for f —
\begin{align} \label{eq:10762a} f &= \frac{c_{tw}}{2 \, \Gamma_{tw} } \\[0.7em]%eqn_interline_spacing &= \small\frac{1}{2} \normalsize \, c_{tw} \, \Gamma_{tw}^{-1} \nonumber \end{align}
Differentiating \( f \) with respect to \( \Gamma_{tw} \) to get the thin-wire tuning rate \( \varphi_{tw} \) —
\begin{align} \label{eq:10763a} \frac{df}{\Gamma_{tw}} = \varphi_{tw} &= -\small\frac{1}{2} \normalsize \, c_{tw} \, \Gamma_{tw}^{-2} \\[0.7em]%eqn_interline_spacing &= -\small\frac{1}{2} \normalsize \, \frac{c_{tw}}{\Gamma_{tw}^2} \nonumber \end{align}
Substituting \( c_{tw} \) from equation \eqref{eq:10760a} into equation \eqref{eq:10763a} —\begin{align} \label{eq:10764a} \varphi_{tw} &= -\frac{f}{\Gamma_{tw}} \end{align}
If the resonator is \( n \) half waves long then the tuning rate is reduced by \( 1/n \) since each tuning slice is effectively divided among each of the \( n \) half-waves —
\begin{align} \label{eq:10765a} \varphi_{tw} &= -\frac{f}{n \, \Gamma_{tw}} \end{align}
Appendix C. Energy stored in a thin longitudinally resonant member
For a longitudinally resonant member whose cross-sectional dimensions are small compared to its half wavelength, the kinetic energy stored in any thin slice \( dx \) is —
\begin{align} \label{eq:10721a} dW &= \small\frac{1}{2} \normalsize \, \dot{u}^2 \, dm \\[0.7em]%eqn_interline_spacing &= \small\frac{1}{2} \normalsize \, \dot{u}^2 \, \left( \rho \, A \, dx \right) \nonumber \end{align}
where —
| \( dW \) | = stored energy in thin slice |
| \( \dot{u} \) | = velocity of slice |
| \( dm \) | = mass of slice |
| \( \rho \) | = density |
| \( A \) | = area of slice |
| \( dx \) | = thickness of slice |
Quarter wave prismatic
For a quarter wave (\( \lambda/4 \)) the kinetic energy can be found by integrating equation \eqref{eq:10721a} over the quarter wave —
\begin{align} \label{eq:10722a} W_{\lambda/4} &= \small\frac{1}{2} \normalsize \, \int_{0}^{\lambda/4}{\dot{u}^2 \, \left( \rho \, A \, dx \right) } \end{align}
For a thin prismatic resonator the amplitude distribution (from the antinodal free end) is —
\begin{align} \label{eq:10723a} u &= U_p \cos \left( {\frac{2\pi}{\lambda}} \, x \right) \, \sin \left( 2\pi f \, t \right) \end{align}
The velocity is the rate of change of the amplitude. Thus, differentiating equation \eqref{eq:10723a} with respect to time gives the velocity distribution —
\begin{align} \label{eq:10724a} \dot{u} &= \frac{du}{dt} \\ &= \left( 2\pi f \right) U_p \, \cos \left( {\frac{2\pi}{\lambda}} \, x \right) \, \cos \left( 2\pi f \, t \right) \nonumber \\ &= \dot{U}_p \, \cos \left( {\frac{2\pi}{\lambda}} \, x \right) \, \cos \left( 2\pi f \, t \right) \nonumber \end{align}
Substituting equation \eqref{eq:10724a} into equation \eqref{eq:10722a} and ignoring the time varying component (to get the maximum energy during the cycle) —
\begin{align} \label{eq:10725a} W_{\lambda/4} &= \small\frac{1}{2} \normalsize \, \int_{0}^{\lambda/4}{\left[ \dot{U}_p \cos \left( {\frac{2\pi}{\lambda}} \, x \right) \right]^2 \, \left( \rho \, A \, dx \right) } \end{align}
For a prismatic resonator the area \( A \) is constant. Also, neither the peak amplitude \( U_p \) nor the frequency \( f \) depend on \( x \). Assume that the density \( \rho \) does not vary with \( x \). Then all of these can be taken outside the integral —
\begin{align} \label{eq:10726a} W_{\lambda/4} &= \small\frac{1}{2} \normalsize \left( \rho \, A\right)\, \dot{U_p}^2 \int_{0}^{\lambda/4}{\left[ \cos \left( {\frac{2\pi}{\lambda}} \, x \right) \right]^2 \, dx } \end{align}
Integrating yields —
\begin{align} \label{eq:10727a} W_{\lambda/4} &= \small\frac{1}{2} \normalsize \left( \rho \, A\right)\, \dot{U_p}^2 {\left[ \frac{x}{2} + \small\frac{1}{4} \normalsize \, \sin \left( {\frac{4\pi }{\lambda}} \, x \right) \right]}_0 ^{\lambda/4} \end{align}
When equation \eqref{eq:10727a} is evaluated for \( x \) between the limits of 0 and \( {\lambda}/4 \), the sin term is 0 at both limits and so drops out. Then equation \eqref{eq:10727a} is —
\begin{align} \label{eq:10728a} W_{\lambda/4} &= \small\frac{1}{2} \normalsize \left( \rho \, A\right)\, \dot{U_p}^2 {\left[ \frac{x}{2} \right]}_0 ^{\lambda/4} \\[0.7em]%eqn_interline_spacing &= \small\frac{1}{2} \normalsize \left( \rho \, A \right)\, \dot{U_p}^2 {\left[ \frac{\lambda}{8} \right]} \nonumber \\[0.7em]%eqn_interline_spacing &= \small\frac{1}{2} \normalsize \left[ \small\frac{1}{2} \normalsize \left( \rho \, A \, \frac{\lambda}{4} \right) \right] \, \dot{U_p}^2 \nonumber \end{align}
The factor in ( ) is just the total mass of the quarter wave section (i.e., \( m_{\lambda/4} \)) so equation \eqref{eq:10728a} can be written as —
\begin{align} \label{eq:10729a} W_{\lambda/4} &= \small\frac{1}{2} \normalsize \left( \frac{m_{\lambda/4}}{2} \right) \, \dot{U_p}^2 \\[0.7em]%eqn_interline_spacing &= \small\frac{1}{2} \normalsize \left( \frac{m_{\lambda/4}}{2} \right) \, \big[ \left( 2\pi f \right) U_p \big]^2 \nonumber \end{align}
Thus, the energy that is cosinually distributed in a prismatic member is the same as if 1/2 of the total quarter-wave mass had been concentrated at the antinode and vibrating with peak velocity \( \dot{U}_p \), corresponding to peak amplitude \( U_p \).
Note that equation \eqref{eq:10729a} could have also been derived from the strain (potential) energy distribution, since at resonance the maximum strain energy equals the maximum kinetic energy.
Half wave prismatic resonator
A half wave (\( \lambda/2 \)) prismatic has twice the mass of a quarter wave prismatic. Therefore it has twice the stored energy of equation \eqref{eq:10729a}—
\begin{align} \label{eq:10730a} W_{\lambda/2} &= \left( \frac{m_{\lambda/2}}{2} \right) \, \dot{U_p}^2 \\[0.7em]%eqn_interline_spacing &= \left( \frac{m_{\lambda/2}}{2} \right) \, \left[ \left( 2\pi f \right) U_p \right]^2 \nonumber \end{align}
Half wave stepped resonator
A half wave resonator with a sharp step exactly at the node can be considered simply as two joined quarter wave resonators — i.e., a quarter wave input section joined to a quarter wave output section. Then from equation \eqref{eq:10729a}—
\begin{align} \label{eq:10731a} _{step}W_{\lambda/2} &= \, _{i}W_{\lambda/4} + \, _{o}W_{\lambda/4} \\[0.7em]%eqn_interline_spacing &= \left[ \small\frac{1}{2} \normalsize \left( \frac{_{i}m_{\lambda/4}}{2} \right) \, _{i}\dot{U}^2 \right] + \left[ \small\frac{1}{2} \normalsize \left( \frac{_{o}m_{\lambda/4}}{2} \right) \, _{o}\dot{U}^2 \right] \nonumber \\[0.7em]%eqn_interline_spacing &= \small\frac{1}{2} \normalsize \left\{ \left[ \left( \frac{_{i}m_{\lambda/4}}{_{o}m_{\lambda/4}} \right) \, \left( {\frac{_{i}\dot{U}}{_{o}\dot{U}}} \right)^2 \right] + 1 \right\} \left( \frac{_{o}m_{\lambda/4}}{2} \right) \, _{o}\dot{U}^2 \nonumber \end{align}
where —
| prefix \( i \) | = input quarter wave |
| prefix \( o \) | = output quarter wave |
A resonator's gain \( G \) is defined as the ratio of output velocity to input velocity (also the ratio of corresponding amplitudes) —
\begin{align} \label{eq:10732a} G = \frac{_{o}\dot{U}}{_{i}\dot{U}} \end{align}
Also, for a resonator with a sharp step at the node, the theoretical gain is the ratio of the mass of the input quarter wave to that of the output quarter wave —
\begin{align} \label{eq:10733a} G = \frac{_{i}m_{\lambda/4}}{_{o}m_{\lambda/4}} \end{align}
Substituting equations \eqref{eq:10732a} and \eqref{eq:10733a} into equation \eqref{eq:10731a} —
\begin{align} \label{eq:10735a} W_{\lambda/2}|_{stepped} &= \small\frac{1}{2} \normalsize \left\{ \left[ G \, \left( \frac{1}{G} \right)^2 \right] + 1 \right\} \left( \frac{_{o}m_{\lambda/4}}{2} \right) \, _{o}\dot{U}^2 \\[0.7em]%eqn_interline_spacing &= \small\frac{1}{2} \normalsize \left( \frac{1}{G} + 1 \right) \left( \frac{_{o}m_{\lambda/4}}{2} \right) \, _{o}\dot{U}^2 \nonumber \end{align}
Comparison to prismatic resonator
Comparing the half-wave stepped resonator of equation \eqref{eq:10733a} to the half-wave prismatic resonator of equation \eqref{eq:10730a} where both are specified to have the same output mass (i.e., the same output cross-sectional area) and the same output velocity —
\begin{align} \label{eq:10736a} \frac{W_{\lambda/2}|_{stepped}}{W_{\lambda/2}|_{prismatic}} = \small\frac{1}{2} \normalsize \left( \frac{1}{G} + 1 \right) \end{align}
Note that when the step disappears (i.e., the input and output quarter-wave sections have the same cross-sectional area so that the gain is just 1.0) the stored energy of the "stepped" resonator (which is then no longer stepped) is just equal to the stored energy of the prismatic resonator, as required.
When the resonator has gain greater than 1.0 then equation \eqref{eq:10736a} shows that the stored energy of the stepped resonator is less than the stored energy of the prismatic resonator. This is dispite the fact that the input section of the stepped resonator must be larger than that of the prismatic resonator in order to provide gain (assuming, again, that both resonators have the same output mass and velocities). It might initially seem odd that a stepped resonator whose input section is more massive than the prismatic resonator would have lower stored energy. However, this occurs because the kinetic energy depends not only on the mass but, also, on the square of the velocity —
\begin{align} \label{eq:10737a} W = \small\frac{1}{2} \normalsize m \, \dot{U}^2 \end{align}
Thus, although the input section is more massive its velocity is correspondingly lower (to provide the required gain) so that the net kinetic energy is lower.
The gain of equation \eqref{eq:10736a} is the highest that is theoretically possible. Practical resonators will have lower gain, either because the step is not sharp (in order to reduce the associated stess) or because the step is not located at the node. Thus, equation \eqref{eq:10736a} gives the highest possible energy reduction for a stepped resonator. Note that, even in the limit as the gain becomes infinite, the energy of the stepped resonator is reduced to only half of that of the prismatic resonator.