Pochhammer Amplitude Distributions in an Infinitely Long Cylinder
In 1876, Pochhammer originally developed the equations for wave propogation in an infinitely long elastic cylinder with isotropic material properties. (Note: the Pochhammer solution is sometimes called the Pochhammer-Chree solution or the Pochhammer-Love solution.)
The following has been taken essentially from Zemanek's (1) analysis.
Axial amplitude distribution
For a cylinder of radius R, the axial amplitude Ua at a radial distance r from the center of the cylinder is given by equation 1. (See Zemanek (1), p. 271, lower equation 18.)
| 1) Ua(r) | = | 2 (γ R)² - Ω² | J1(k R) J0(h r) + | 2 (k R) (h R) J1(h R) J0(k r) |
where:
| 1a) γ | = | 2π f |
| C |
| 1b) Ω | = | 2π f R |
| Cs |
| 1c) h | = | 2π f | 1 | - | 1 | ½ | ||
| Cd² | C² |
| 1d) k | = | 2π f | 1 | - | 1 | ½ | ||
| Cs² | C² |
| 1e) Cs | = | Ctw | 1 | ½ | ||
| 2 (1 + ν) |
| 1f) Cd | = | Ctw | 1 - ν | ½ | ||
| (1 + ν) (1 - 2ν) |
| R | = radius of cylinder |
| r | = radius at which the amplitude will be evaluated |
| f | = frequency |
| C | = wave speed of the cylinder whose radius is R |
| Cs | = shear wave speed |
| Cd | = dilitational wave speed |
| Ctw | = thin-wire wave speed |
| ν | = Poisson's ratio |
| J0 | = Bessel function of the first kind, order 0 |
| J1 | = Bessel function of the first kind, order 1 |
Each Bessel function operates on the parameter in ( ) (i.e., the Bessel function argument). (See below for further notes on Bessel functions.)
Cs and Cd can be evaluated from various material constants. (See the chapter on "Wave Motion".) However, unlike Cs and Cd, C is not a material constant. Instead, C depends on the cylinder diameter. For the chosen cylinder diameter, C can be determined from the Pochhammer frequency equation. (See Zemanek (1), p. 267, equation 6. Also see the chapter on "Wave Motion".) However, the solution of this equation is difficult. Instead, C can more easily be determined by the Mori equation. (See the chapter on "Wave Motion".)
Note that both Cs and Cd depend on Poisson's ratio ν. Hence, the axial amplitude distribution, as well as the radial amplitude (below) will also depend on Poisson's ratio.
In the above equation, if r = 0 then U represents the axial amplitude at the axis of the cylinder. For r = 0 two of the Bessel functions evaluate to 1:
| J0(h r) | = | J0(0) = 1 |
| J0(k r) | = | J0(0) = 1 |
Then, the axial amplitude at the center of the cylinder is:
| 2) Ua(r=0) | = | 2 (γ R)² - Ω² | J1(k R) + | 2 (k R) (h R) J1(h R) |
If equation 1 is evaluated at r and divided by equation 2, the result is Ŵ(r) (i.e., the uniformity at radius r):
| 3) Ŵ(r) | = | Equation 1 @ r | 100 | ||
| Equation 2 |
If equation 3 is evaluated at various radius locations, a typical result is shown in figure 1.
 |
| Figure 1. Pochhammer Uniformity Across the Face of a Ø125 mm Al 7075‑T6 Cylinder |
Evaluating equation 3 at R (the cylinder periphery) gives the overall uniformity Ŵ.
| 4) Ŵ | = | Equation 1 @ R | 100 | ||
| Equation 2 |
If equation 4 is evaluated for cylinders of various diameters, a typical result is shown in figure 2.
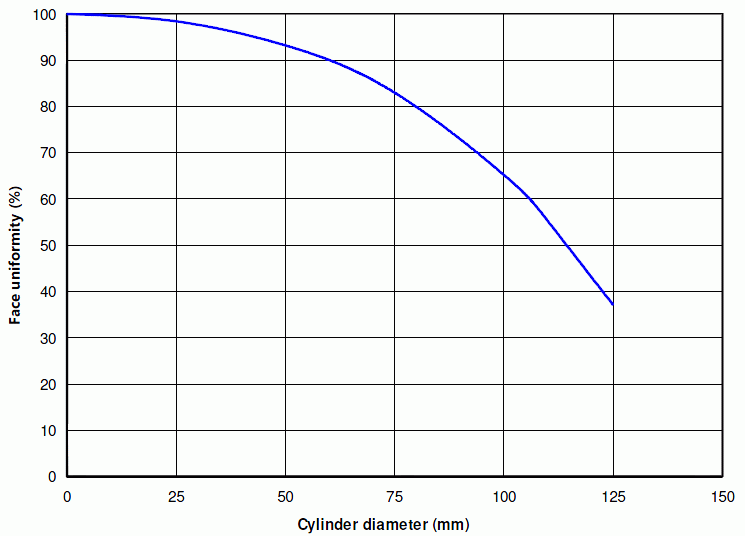 |
| Figure 2. Pochhammer Face Uniformity for a Al 7075‑T6 Cylinder |
Radial amplitude distribution
For a cylinder of radius R, the radial amplitude Ur at a radial distance r from the center of the cylinder is given by equation 1. (See Zemanek (1), p. 271, upper equation 18.)
| 5) Ur(r) | = | h |
|
|||||||||||||
| γ |
At the periphery of the cylinder (r = R) the above equation becomes:
| 6) Ur(r=R) | = | h |
|
|||||||||||||
| γ |
If equation 6 is divided by equation 2 then the result is the relative radial amplitude (as a percent of the axial centerline amplitude):
| 7) Ŵr | = | Equation 6 @ R | 100 | ||
| Equation 2 |
It turns out that the numerator and denominator of this equation have opposite signs. This indicates that when the face is moving outward the node is collapsing inward and vice versa. This is expected from Poisson coupling.
Note: see appendix B for a simpler cubic equation that approximates equation 7.
(Note: See Mori for other equations that approximate the face amplitude distribution in a cylindrical horn.)
Maximum applicable diameter for half-wave horns
The Pochhammer equation was developed for an infinitely long cylinder. However, cylindircal horns have finite length. It turns out that the Pochhammer equation is valid for cylindrical horns as long as the shear stresses are small compared to the longitudinal stresses. This will be true if the horn diameter is not excessively large compared to the tuned half-wavelength. Zemanek (1) (pp. 272 - 275) shows that the shear stresses remain less than 1% of the longitudinal stress as long as Ω < 2.6 (p. 275)). (Also see Thurston, p. 16.) Substituting this value and Cs (equation 1e) into equation 1b and solving for D (i.e., 2R) gives:
| 8) D | ≤ | Γtw | 5.2 | 1 | ½ | |||||
| π | 2 (1 + ν) |
| 8) D | ≤ | Ctw | 5.2 | 1 | ½ | ||||||||
| 2 f | π | 2 (1 + ν) |
where:
| D | = diameter of cylinder |
| f | = frequency |
| Ctw | = thin-wire wave speed |
| Γtw | = material thin-wire half-wavelength |
| ν | = Poisson's ratio |
Using the material constants for Al 7075‑T6 aluminum (Ctw = 5081 m/sec, ν = 0.33), the above equation indicates that the maximum diameter for which the Pochhammer equation is valid for this aluminum at 20 kHz is approximately 130 mm. Above 130 mm, the Pochhammer equation will have increased error. In fact, the Pochhammer equation predicts that the aluminum horn will a node at 150 mm. This is obviously incorrect, since an axial resonance should never have a face node (except when influenced by an adjacent nonaxial resonance).
In addition to the limiting diameter, the Pochhammer equation also assumes that the rod material is homogeneous. Therefore, it does consider the effect of a stud.
Appendix A — Bessel Functions
The important Bessel functions for the Pochhammer equation have the following characteristics (see Kinsler, appendix A4, pp. 449 - 452):
- J0(X), where X is a real number — The J0(X) function resembles a decaying cosine function and has a maximum value of 1.0.
- J0(jX), where jX is an imaginary number — The J0(jX) function is real valued and resembles a hyperbolic cosine function, whose value rapidly increases as X increases. J0(jX) can be expressed as a modified Bessel function (Kinsler, p. 450):
where Io(X) is real valued.J0(jX) = I0(X) - J1(X), where X is a real number — The J1(X) function resembles a decaying sine function and has a maximum value of about 0.58.
- J1(jX), where jX is an imaginary number — The J1(jX) function is imaginary and resembles a hyperbolic cosine function, whose value rapidly increases as X increases. J1(jX) can be expressed as a modified Bessel function (Kinsler, p. 450):
where I1(X) is real valued.J1(jX) = j I1(X)
For longitudinal resonators that are of interest in high-power ultrasonics, Cd is always greater than C. Thus, h is imaginary since the value under the √ is negative. Thus, (h R) and J1(h R) are both imaginary and their product in the above equations is thus a negative real number.
Appendix B — Polynomial Curve-fit
While equation 4 well with measured uniformities, it can be cumbersome to calculate. Therefore, a cubic polynomial equation has been fitted:
| B1) Ŵ | = |
|
100 |
where:
| Ŵ | = cylinder uniformity for specified cylinder diameter |
| D | = cylinder diameter |
| Γtw | = thin-wire half-wavelength |
| b2, b3 | = curve fit constants |
Note that as the cylinder diameter goes to zero the uniformity goes to 100%, as required. Also, since the slope of the uniformity curve should be zero when the horn diameter is zero, the equation has no linear term (D/Γtw)¹ .
The thin-wire half-wavelength Γtw is calculated from the equation:
| B2) Γtw | = | Ctw |
| 2 f |
Equation B‑1 was fitted to the Pochhammer equation for 7 diameters ranging between 0 and 125 mm at a frequency of 20000 Hz and a wave speed of 5081 (corresponding to Al 7075‑T6 aluminum). This yielded the curve-fit constants:
| B3a) b2 | = -0.24744 |
| B3b) b3 | = -0.40538 |
with a the standard error of estimate 0.32.
The curve from equation B1 with the fit constants from B3a and B3b is graphed in figure B1.
 |
| Figure B1. Pochhammer Face Uniformity for a Al 7075‑T6 Cylinder |
Because of the nondimensional form of equation B1, it is also valid at frequencies other than 20 kHz and for wave speeds other than 5081 m/sec. However, the uniformity will err if Poisson's ratio varies significantly from 0.33. Fortunately, most acoustic materials have Poisson's ratios between 0.29 and 0.34, so that equation B1 will give reasonable results for these materials.